1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
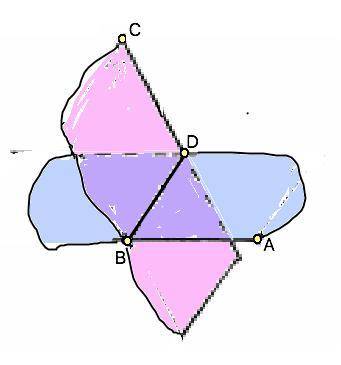
Прямые АВ и СD не лежат в одной плоскости. По какой прямой пересекаются плоскости ABD и ВСD?
ответ: По прямой ВD.
Объяснение. Плоскости ABC и ВСD имеют две общие точки: В и D.
Из аксиом планиметрии:
1.Через любые две точки можно провести прямую, притом только одну.
Из аксиом стереометрии:
2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следовательно, все точки прямой ВD лежат и в плоскости ABD, и ВСD, т.е. эти плоскости пересекаются по прямой ВС,
ответ:34,98 см²
Объяснение:
Из суммы углов треугольника найдем
∠М=180°-(∠K+∠L)=180°-(30°+65°}=85°
По т.синусов КL:sin85°=KM:sin65° ⇒
KL=KM•sin85°/sin65°
KL=13•0,9063:0,99619≈11,82696≈11,83 см
Одна из формул площади треугольника
S=a•b•sinα:2, где а и b - стороны треугольника, α- угол между ними.
S(KLM)=KM•KL•sin30°:2
S(KLM)=13•11,83•0,5:2≈34,98 см²