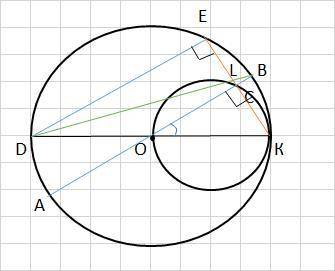
Объяснение:
∠DEK опирается на диаметр DK большой окружности.
∠ОВК опирается на диаметр ОК малой окружности.
Все вписанные углы, опирающиеся на диаметр, прямые. Следовательно,
∠DEK = ∠ОВК = 90°. Из этого следует, что
DE ⊥EK и АВ ⊥ЕК.
Теорема: если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны. Значит, DE ║ АВ, ч.т.д.
б) Так как DE ║ АВ, то ∠ВОК = ∠ЕDК как соответственные.
Диаметр АВ ⊥ЕК. Если хорда перпендикулярна диаметру, то диаметр проходит через её середину, т.е.
ЕС = СК и т. В - середина дуги ЕК и, следовательно,
DB - биссектриса ∠EDK прямоугольного ΔDEK.
Теорема: Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон, т.е.
ЕL : LK = DE : DK = cos(∠KDE) = cos(∠KOB) = √(1 - sin²(∠KOB) =
= √1 -7/16 = √9/16 = 3/4
Відповідь:
Стороны начального прямоугольника:
а = 6 см., в = 8 см.
Стороны нового прямоугольника:
а = 12 см., в = 6 см.
Пояснення:
Пусть стороны начального прямоугольника а и в, тогда первое уравнение:
2а + 2в = 28
а + в = 14
В новом прямоугольнике а увеличилось на 6, а в уменьшилось на 2.
Площадь начального прямоугольника:
а × в
Площадь нового прямоугольника:
(а + 6) × (в - 2)
Получаем второе уравнение:
(а + 6) × (в - 2) = а × в + 24
а × в + 6в - 2а -12 = а × в + 24
6в - 2а = 36
Из первого уравнения:
в = 14 - а
Подставляем в во второе уравнение:
84 - 6а - 2а = 36
8а = 48
а = 6 см.
Подставляем первое уравнение:
в = 14 - 8
в = 8 см.
Стороны начального прямоугольника:
а = 6 см., в = 8 см.
Стороны нового прямоугольника:
а = 6 + 6 = 12 см.
в = 8 - 2 = 6 см.
Проверка:
12 × 6 = 8 × 6 + 24
72 = 48 + 24
72 = 72
Решение смотрите во вложении