ответ: 298. 32 см, 72см, 56см.
292. 23 дм.
Объяснение:
"298. Периметр треугольника равен 80 см. Стороны треугольника, образованного средними линиями данного треугольника, относятся как 4:9:7. Найдите стороны данного треугольника."
***
Пусть одна сторона треугольника, образованного средними линиями трапеции равна 4х. Тогда вторая будет 9х, а третья - 7х. Периметр этого треугольника равен 80 см.
Р=4х+9х+7х=80;
20х=80;
х=4;
4x=4*4=16 см;
9х=9*4=36 см;
7х=7*4=28 см;
Проверим:
Р=16+36+28= 80 см. Всё верно!
Средние линии треугольника равны половине основания. Значит основания равны удвоенным средним линиям.
Одна сторона равна 2*16=32 см;
Вторая сторона равна 2*36=72 см;
Третья сторона равна 2*28=56 см.
***
"292.Стороны треугольника равны 12 дм, 16 дм и 18 дм. Найдите периметр треугольника, сторонами которого являются средние линии этого треугольника."
***
АВС - треугольник. MNP - треугольник, образованный средними линиями треугольника. Каждая из них равна половине стороны ей параллельной.
MN=BC/2=16/2=8 дм.
NP=AC/2=18/2=9 дм.
MP=AB/2 =12/2=6 дм.
Р MNP=8+9+6= 23 дм.
Найти периметр трапеции по готовому чертежу
Объяснение:
∠BCО = ∠ОЕА= 30° как накрест лежащие , при секущей СЕ.
По т. о внешнем угле треугольника в ΔЕАО , ∠ЕОА=60°-30°=30°. Откуда ∠AOE = ∠BOC = 30° ⇒ ∠ВОС=30°.
Значит ΔЕАО=ΔСВО по стороне и 2-м прилежащим углам:
ОА=ОВ по условию,
∠AOE = ∠BOC = 30° ,
∠ЕАО=∠СВО как накрест лежащие ,АВ-секущая.
В равных треугольниках соответственные элементы равны ⇒ЕА=ВС.
Пусть ЕА=ВС=а. Т.к. ΔЕАО , ΔСВО-равнобедренные , то ЕА=ОА=ВС=ОВ=а . Тогда сторона трапеции АВ=2а ⇒ СD=2а (*),
т.к АВСD-равнобедренная трапеция( ∠D=180°-120°=60°)
Из Δ ECD -прямоугольный , ЕD=ЕА+АD=а+15 найдем C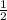D = 
ED =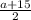
(**).
Приравняем полученные выражения (*) и (**) , получим
2а =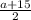 , 4а=а+15 , а=5 ⇒ ВС=5, АВ=СD=10
P(ABCD) = 5 + 15 +2* 10 =40 .
Два угла треугольника равны 40° и 52°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов.
- - -
Дано :ΔАВС.
∠А = 40°.
∠В = 52°.
ВН₁ и АН₂ - высоты.
Точка О - ортоцентр (точка пересечения высот).
Найти :∠АОВ = ? (или ∠Н₁ОН₂, не важно, так как они равны как вертикальные).
Решение :Немного о расположении ортоцентра О :
Для начала найдём ∠С.
По теореме о сумме углов треугольника -
∠А + ∠В + ∠С = 180°
∠С = 180° - ∠А - ∠В
∠С = 180° - 40° - 52°
∠С = 88°.
Так как все углы ΔАВС - острые, то ортоцентр О лежит внутри ΔАВС.
- - -
Рассмотрим ΔСВН₁ - прямоугольный (так как ∠ВН₁С = 90° по определению высоты треугольника).
Сумма острых углов прямоугольного треугольника равна 90°.Тогда -
∠Н₁СВ + ∠Н₁ВС = 90°
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - 88°
∠Н₁ВС = 2°.
Теперь рассмотрим ΔОВН₂ - прямоугольный (так как ∠ОН₂В = 90°).
По выше сказанному -
∠ВОН₂ + ∠ОВН₂ = 90°
∠ВОН₂ = 90° - ∠ОВН₂
∠ВОН₂ = 90° - 2°
∠ВОН₂ = 88°.
- - -
∠ВОН₂ и ∠АОВ - смежные.
Сумма смежных углов равна 180°.Следовательно -
∠ВОН₂ + ∠АОВ = 180°
∠АОВ = 180° - ∠ВОН₂
∠АОВ = 180° - 88°
∠АОВ = 92°.
ответ :92°.