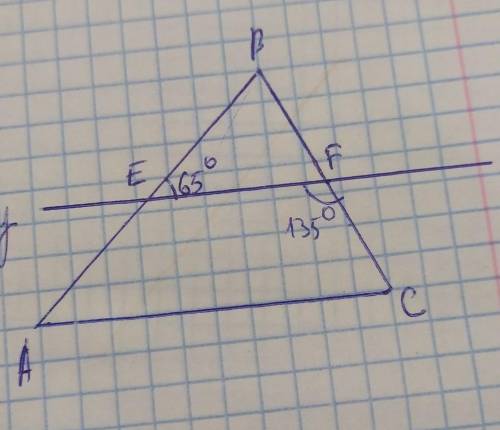
Угол A равен 65 градусов, угол B равен 70 градусов, угол C равен 45 градусов.
Объяснение:
Т. К. Углы BFE и EFC смежные, то угол бфе равен 180-135=45 градусов. Углы BEF и FEA смежные, значит угол феа равен 180-65=115 градусов. Рассмотрим треугольник EBF, т. К. Сумма всех углов равна 180 градусов. Тогда угол EBF равен 180-65-45=70 градусов. Рассмотрим две параллельные прямые EF и AC, секущая AB, тогда в углы EAC и BEF равны как соответственные, тоже самое и с другой стороны, только секущая BC. Тогда выясним, что угол EAC равен 65 градусов, а угол FCA 45 градусов.
- правильная треугольная пирамида SABC,
- высота пирамиды SO = Н,
- угол наклона бокового ребра L к основанию равен α .
Примем сторону основания за а.
Проекция AO бокового ребра AS на основание правильной пирамиды равна 2/3 высоты h основания.
Из треугольника ASO находим AO = H/tg α.
Высота h в 1,5 раза больше АО, то есть h = (3/2)H/tg α = 3H/(2tg α),
тогда сторона а основания равна:
а = h/(cos30°) = 3H/(2tg α)/(√3/2) = √3H/tg α.
Площадь основания So = a²√3/4 = 3√3H²/(4tg² α) кв.ед.
Тогда объём пирамиды равен:
V = (1/3)SoH = (1/3)*(3√3H²/(4tg² α))*H = √3H³/(4tg² α) куб.ед.
2) Дано:
правильная четырёхугольная пирамида SABCД,
- высота пирамиды SO = Н,
- угол наклона бокового ребра L к основанию равен α .
Половина ОА диагонали АС равна Н/tg α.
Тогда сторона а основания а = Н√2/tg α.
So = a² = 2H²/(tg² α).
V = (1/3)*(2H²/(tg² α))*H = 2H³/(3tg² α).