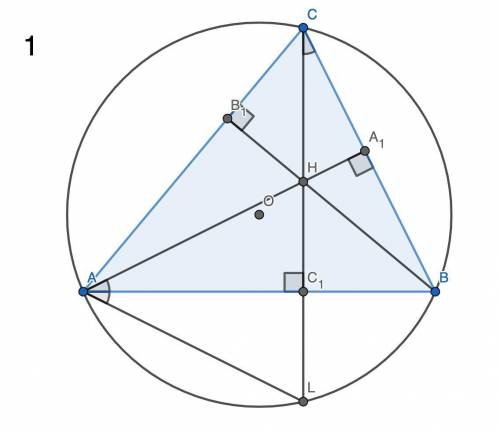
1) В треугольниках ΔAA₁B и ΔСС₁B углы ∠A₁ и ∠C₁ — прямые, угол ∠B — общий. Значит, углы ∠A₁AB и ∠С₁CB (∠LCB) равны (так как все углы каждого треугольника должны в сумме давать 180°).
Углы ∠LAB и ∠LCB опираются на одну дугу, значит, они равны.
∠A₁AB = ∠LCB, ∠LCB = ∠LAB ⇒ ∠A₁AB = ∠LAB. Тогда прямоугольные треугольники ΔAC₁H и ΔAC₁L равны по общему катету AC₁ и прилежащему к нему углу (∠A₁AB = ∠LAB). Значит, их соответствующие элементы равны, в частности, HC₁ = C₁L, что и требовалось доказать.
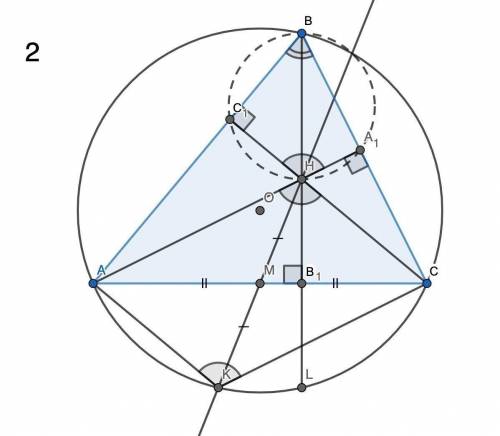
2) AM = MC, HM = MK по условию ⇒ AKCH — параллелограмм ⇒ ∠AKC = ∠AHC. ∠AHC = ∠A₁HC₁ как вертикальные ⇒ ∠AKC = ∠A₁HC₁.
∠BA₁H = ∠BC₁H = 90° (в сумме дают 180°) и опираются на один отрезок (лежат по разные стороны этого отрезка). Значит, около четырёхугольника A₁BC₁H можно описать окружность. Но тогда ∠A₁HC₁ = 180° - ∠A₁BC₁. А поскольку ∠AKC = ∠A₁HC₁, то ∠AKC = 180° - ∠A₁BC₁. Значит, четырёхугольник ABCK — вписанный, K лежит на описанной около ABC окружности, что и требовалось доказать.
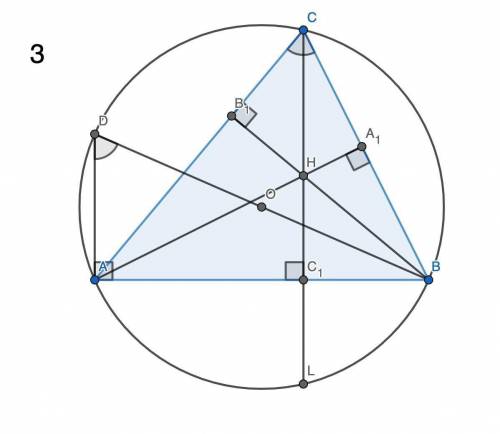
3) Продлим BO до пересечения с окружностью в точке D — получим диаметр BD. Тогда ∠BAD — прямой, так как опирается на диаметр. В треугольниках ΔBAD и ΔBB₁C: ∠BAD = ∠BB₁C = 90°, ∠ADB = ∠ACB как опирающиеся на одну дугу. Значит, углы ∠ABD и ∠CB₁B также равны. Но это те же углы, что и ∠ABO и ∠CBH соответственно. Значит, ∠ABO = ∠CBH, что и требовалось доказать.
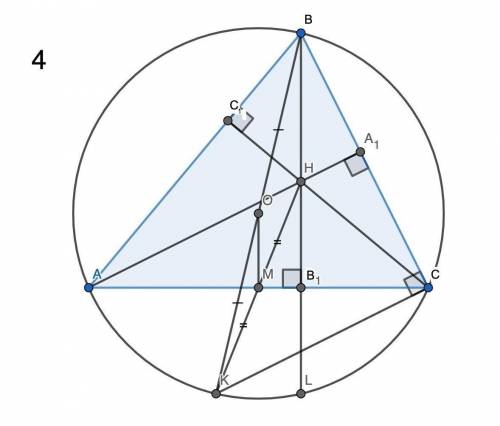
4) Пусть HM = MK. Тогда K лежит на описанной окружности по п. 2. Также по п. 2 AKCH — параллелограмм ⇒ AH║KC, но AH⊥BC ⇒ KC⊥BC. ∠KCB — прямой, значит, KB — диаметр ⇒ KO = OB.
Рассмотрим ΔKOM и ΔKBH: ∠K — общий, KO : KB = 1 : 2, KM : KH = 1 : 2 по построению ⇒ треугольники подобны ⇒ OM : BH = 1 : 2 ⇒ BH = 2OM, что и требовалось доказать.
2.
треугольникк это фигура которая состоит из трёх углов и трех прямых соединенных между собой в замкнутую цепь.треугольники бывают трех видов остроугольные тупоугольные и прямоугольные у остроугольных есть один угол как минимум который от 0 до 90 градусов у тупоугольного от 90 до 180 у прямоугольного есть хотя бы один угол 90 градусов по сторонам треугольники из трёх видов это равносторонние и равнобедренные и равносторонние разносторонний этого треугольника у которых длина сторон разные равнобедренная Когда две стороны равны между собой и равносторонние либо правильная треугольнике это те треугольники у которых все углы по 60 градусов и все стороны равны
3.
во всех треугольников будет сумма острых углов 90 градусов так как сумма всех углов треугольника 180 градусов и так как в прямоугольном треугольнике есть один угол 90 градусов то два других в сумме будут 180 - 90 равно 90.
номер 2
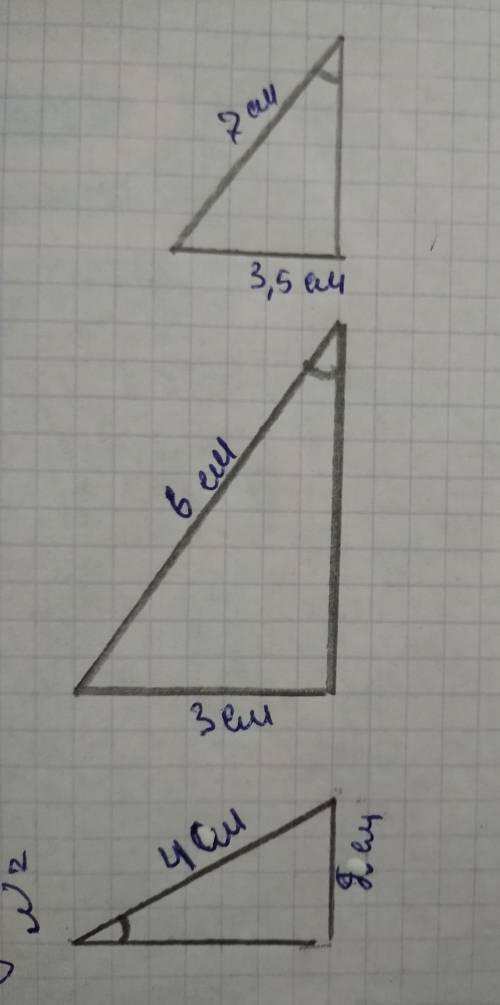
вывод: в каждом треугольнике есть угол 90 градусов и угол 30 градусов а значит что каждый острый угол будет равен 60 градусов так как сумма углов будет 180 градусов.длина катета зависит от гипотенузы и угла в 30 градусов.Катет лежащий против угла в 30 градусов равен половине гипотенузы. Дан треугольник у которого есть угол 90 градусов и 30 градусов То третье угол будет равен 60 так как сумма острых углов равна 90 и 90 - 30 равно 60 если Дан угол 30 градусов то второй угол равен 60 так как 90 минус 30 равно 60 - это тоже самое ссвойство.есть еще одно свойство про угол 30 градусов катет лежащий против угла в 30 градусов равен половине гипотенузы либо же наоборот половине гипотенузы равен катет лежащий против угла 30 градусов но 1 мне кажется легче.
остальное задание будет на фото

k=(3 3/11+1 8/11):9
k=5/9