В задании на рисунке две прямых с.
Изменив рисунок, получаем: прямая d пересекает три прямые a, b и с.
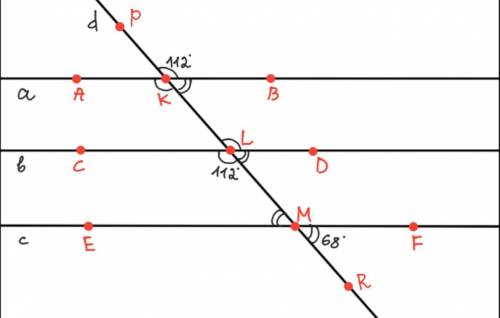
Чтобы была возможность именовать углы, обозначим на прямых точки A, B, C, D, E, F, K, L, М, Р и R (см. рисунок).
Не забываем: )
Если при пересечении двух прямых секущей накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые параллельны.
1) Вертикальные углы при пересечении двух прямых всегда равны, а это значит:
∠РКВ=∠AKL=112°,
∠KLD=∠CLM=112°,
∠EML=∠RMF=68°.
2) Как видим из предыдущего пункта, ∠PKB=∠KLD=112° ⇒ прямые a и b параллельны, т.к. углы равны как соответственные, а прямая d — секущая.
3) Прямые b и c тоже параллельны, покажем это.
Известно, что ∠CLM=122°, ∠EML= 68°.
∠CLM+∠EML=122°+68°=180°.
Согласно теореме, если две прямые при пересечении секущей параллельны, то их односторонние углы в сумме составляют 180°.
∠CLM+∠EML=180° ⇒ прямые b и c параллельны! (т.к. сумма одностор. углов 180°, прямая d — секущая)
4) Из 2 и 3 пунктов известно, a||b и b||c ⇒ a||c ⇒ a||b||c.
ответ: прямые а, b и с параллельны.
r = (1/2) / cos 30° = (1*2) / (2*√3) = 1 / √3.
Высоту тетраэдра находим по Пифагору:
H = √(1² - (1/√3)²) = √(2/3).
Теперь рассмотрим осевое сечение шара, проходящее через ребро тетраэдра.
Высота в прямоугольном треугольнике (она же радиус r), проведенная из вершины прямого угла, делит его на два подобных.
Из подобия запишем пропорцию:
H/1 = 1/D. Отсюда D = 1/H = 1 / (√(2/3)) = √(3/2).
Объём шара равен V = (1/6)π*D³ = (1/6)π*(3/2)*(√(3/2) = 0,96191.