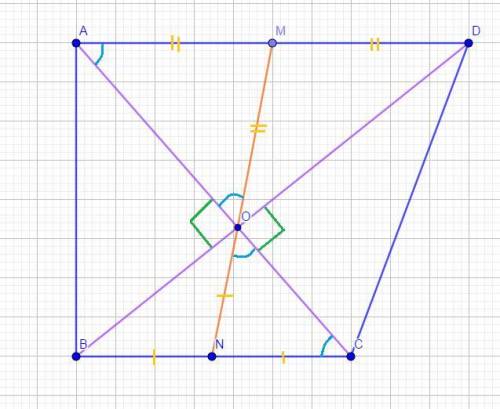
Четырехугольник ABCD, O - точка пересечения диагоналей,
AD || BC и AC ⊥BD,
M - середина AD, N - середина BC,
AD = 12 и BC = 7 (смотрите рисунок).
Найти:Длина отрезка MN.
Решение:Заметим, что O ∈ MN, так как угол MON - развернутый:
∠MON = ∠DOC + (∠DOM + ∠CON) = 90° + (∠OCB + ∠OBC) =
= 90° + 90° = 180°.
Значит, нам достаточно найти длину MO + NO.
Так как треугольник AOD прямоугольный, то медиана MO, проведенная из вершины прямого угла к гипотенузе, равна половине этой гипотенузы (по свойству медианы прямоугольного треугольника):
MO = AD / 2 = 12 / 2 = 6.
Тоже самое можно сказать и о прямоугольном треугольнике BOC с медианой NO:
NO = BC / 2 = 7 / 2 = 3,5.
Значит:
MO + NO = MN = 6 + 3,5 = 9,5.
ответ:MN = 9,5 .
Сечение amb, площадь которого надо найти - равнобедренный треугольник с основанием ab и боковыми сторонами am и bm. Основание нам дано - это сторона основания пирамиды, равная 8. Боковые грани - равные равнобедренные треугольники. Значит углы при вершинах граней равны 36°, равны и все углы при основании граней (180°-36°):2 = 72°.
В треугольнике asm <asm=36°(дано), <sam=36°(как половина угла sac=72°) и <amb=(180°-72°)=108°. Углы ams и amc смежные. Тогда <amc=180°-108°=72° и значит треугольник amc равнобедренный и am=ac=8. Но am=bm, а ac=ab. Значит сечение - правильный треугольник и его площадь равна:
Sabm = (√3/4)*a², где а - сторона треугольника.
Итак, Sabm = (√3/4)*64 = 16√3.