Вспомним теорему:
В прямоугольном треугольнике напротив 30° лежит катет равный половине гипотенузы
В нашем случае наоборот, АС это катет который находится против 30° значит гипотенуза будет в два раза больше. 20см
ответ:20см
ответ: 6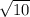
Объяснение: Итак AC=7 и BD=6 - диагонали трапеции, AD= 8 и ВС=3 - основания трапеции. Проведем через С отрезок СК параллельный BD , где К- точка пересечения с прямой основаня AD. Имеем треугольник АСК со сторонами АС=7, СК=6, АК= 8+3=11.
DK=ВС=3, так как ABDK- параллелогамм по построению.
Заметим, что площадь треугольника АСК равна площади трапеции ABCD, т.к. треугольник ACD общий , а треугольники АВС и CDK имеют одинаковую площадь. ( ВС=DK - основания треугольников, а высота, проведенная к основанию у обоих треугольников есть высота трапеции ABCD, т.е. тоже равны)
Найдем площадь треугольника АСК по теореме Герона.
Sack= 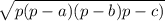 =
= 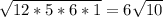
p= (7+6+11)/2=12
На сторонах прямоугольного треугольника АВС (<C=90°) построены квадраты. Площадь квадрата, построенного на гипотенузе, равна 400 см², а разница площадей квадратов, построенных на катетах, равна 112 см² .Найти площадь треугольника.
Объяснение:
Пусть катет АС=у , ВС=х, при чем х>0 ,y>0 .
По т Пифагора для ΔАВС х²+ у²=400.
С другой стороны S1=у², S2=х² и по условию S2- S1=112.
Тогда х²-у²=112. Получили систему
{ х²+ у²=400,
{ х²-у²=112. Почленно сложим х²=256 , x=16,
Почленно вычтем , получим у²=144, у=12.
S( треуг)=1/2*а*в, где а,в- длины катетов.
S( треуг)=1/2*12*16=96(см²)
С=90°, В = 30°, А=60° АВ=20см
Объяснение:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Теорема, обратная теореме Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный