Для решения данной задачи, нам понадобятся знания из геометрии и теории треугольников.
1. Найдем длину диагонали параллелепипеда. Здесь нам поможет третья сторона прямоугольного треугольника, образованного гранями параллелепипеда. Для нахождения этой стороны можно воспользоваться теоремой Пифагора:
a^2 + b^2 = c^2,
где a и b - катеты, а c - гипотенуза треугольника.
В нашем случае a = 9, b = 12, поэтому:
9^2 + 12^2 = c^2,
81 + 144 = c^2,
225 = c^2.
Чтобы найти длину диагонали, нужно извлечь из равенства квадратный корень:
c = √225,
c = 15.
Таким образом, длина диагонали параллелепипеда равна 15.
2. Для нахождения угла между диагональю и плоскостью основания, воспользуемся знанием о свойствах взаимно перпендикулярных плоскостей. Если диагональ параллелепипеда перпендикулярна плоскости основания, то угол между этими плоскостями равен 90 градусов.
Таким образом, угол между диагональю и плоскостью основания равен 90 градусам.
Следует отметить, что для понимания и решения подобных задач необходимо знание основ геометрии и треугольников, а также умение применять эти знания на практике.
1. Для начала, давайте взглянем на данную нам фигуру. У нас есть правильная четырёхугольная пирамида SABCD с вершиной S и центром основания O. Также нам известно, что SC = 35 и BD = 42.
S
/|\
A-B-C
| |
D---O
2. Чтобы найти длину отрезка SO, нам необходимо разбить эту задачу на несколько более простых шагов. Для начала, давайте найдем длину отрезка OC.
3. Поскольку пирамида SABCD является правильной, каждая сторона основания равна друг другу. Если SC = 35, то SA = SB = 35.
4. Мы знаем, что O – центр основания, то есть точка пересечения диагоналей AB и CD. Это означает, что OC – это половина диагонали AB.
5. Раз диагональ AB – это сторона правильного четырёхугольника, то AB = 35.
6. Следовательно, OC = AB / 2 = 35 / 2 = 17.5.
7. Теперь мы можем найти длину отрезка SO. Поскольку SO – это диагональ пирамиды SABCD, то он является диагональю основания SBC и проходит через центр основания O.
8. Так как основание SBC – это правильный треугольник, то SO будет равен двум разом длине OC (SO = 2 * OC).
9. Отсюда, SO = 2 * 17.5 = 35.
10. Итак, длина отрезка SO равна 35.
Это подробное решение поможет школьнику понять, как мы пришли к ответу и какие шаги были предприняты для решения задачи.
Відповідь:
BC = 2 × MC = 2 × 15 = 30
BM = =
=  =
=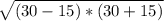 =
= 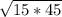 =
= 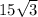
Пояснення: