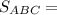4см²
Объяснение:
Смотри прикреплённый рисунок.
О - точка пересечения медиан АМ и BN.
Медианы треугольника точкой пересечения О делятся в отношении 2:1, считая от вершины, поэтому BO =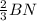 
= 2 см, NO = 
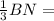1 cм.
Проведём линию MN, соединяющую середины сторон АС и ВС.
MN = 0.5AB, поскольку MN - средняя линия треугольника.
ΔNMC ~ ΔABC по двум углам (∠С - общий, ∠СMN = ∠СBA как соответственные при MN || AB и секущей ВС)
Коэффициент подобия k = MN: AB = 0,5, поэтому площади ΔNMC и ΔABC относятся, как k² = 0.25.
Тогда площадь трапеции ABMN составляет 0,75 площади ΔABC.
Вычислим площадь трапеции ABMN.
.
.
.
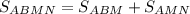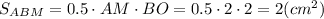
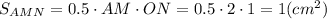
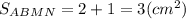
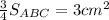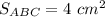Відповідь: СМ=6 см
Пояснення:
Дано:
ΔАВС - равнобедренной
АВ=16 см - основание
АС=10 см
СМ - медиана
Найти: СМ-?
Решение
Так как СМ - медиана, АМ=МВ=18:2=8 (см)
Так ΔАВС равнобедренной, медиана является и высотой.
Рассмотрим ΔАМС - прямоугольный
За теоремой Пифагора АС²=АМ²+СМ²
Отсюда СМ²=АС²-АМ²
СМ²=10²-8²=100-64-36 (см²)
СМ=6 (см)
Рисовать в Паинте умею не очень, так что как-то так