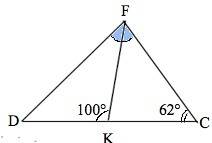
Угол FKD для ∆FKC- внешний и равен сумме двух несмежных с ним углов.
62°+CFK=100°
CFK=100°-62°=38°
FK- биссектриса, след. угол ВАС=2₽38°=76°
* * *
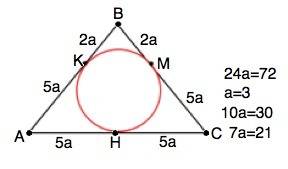
Отрезки касательных, проведенных из одной точки, равны.
АК=АН,ВК=ВМ, СК=СМ.
Примем коэффицинент отношения отрезков сторон равным а. Тогда АН=АК=5а, СН=СМ=5а,
ВК=ВМ=2а
Периметр ∆ АВС=24а
24а=72а
а=3
АВ=ВС=3•(2+5)=21 см,
АС=3•(5+5)=30см
* * *
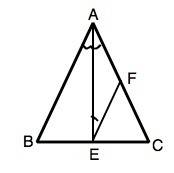
Треугольник АВС - равнобедренный.
АF=FE. ∆ АЕF – равнобедренный, угол ЕАD=AFE.
АЕ - высота равнобедренного треугольника, она же – его медиана и биссектриса.
∠ВАЕ=∠АЕF. эти углы - накрестлежащие. Если при пересечении двух прямых накрестлежащие углы равны. эти прямые - параллельны.
EF || АВ, ч.т.д.
1) O₁C||O₂A, т.к. ∠O₁CA=45°+∠BCA, ∠O₂AC=45°+∠DAC, ∠DAC=∠BCA, т.е. внутр. накрест лежащие углы ∠O₁CA и ∠O₂AС равны.
2) Значит треугольники O₁CO' и O₂AO' подобны (по двум углам), т.е.
CO'/AO'=CO₁/AO₂=(BC/√2)/(AD/√2)=BC/AD.
3) Но О тоже делит AC в отношении BC/AD, т.к. треугольники BCO и DAO подобны. Значит O' совпадает с O.