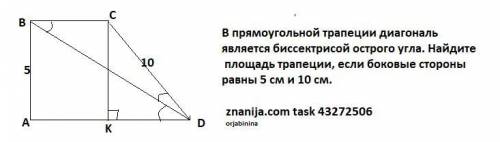
В прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите площадь трапеции, если боковые стороны равны 5 см и 10 см.
Объяснение:
ABCD-прямоугольная трапеция . Перпендикуляр AB=5cм, наклонная CD=10 см . Пусть СК ⊥АD, тогда АВСК-прямоугольник и АВ=СК=5 cм.
ВD- биссектриса , значит ∠АDВ=∠ВDС. Но ∠АDВ=∠DВС как накрест лежащие, при ВС||АD ,BD-секущая.
Поэтому ∠DВС=∠ВDС а это означает, что ΔВDС- равнобедренный ⇒ BC=CD=10 см.
ΔCKD-прямоугольный , по т. Пифагора KD=√(10²-5²)=√(5*15)=5√3 .
Тогда AD=10+5√3 ( см). Формула S (трапеции) =1/2*h*(a+b) ,
S (АВСD) =1/2*5*(10+10+5√3)=12,5(4+√3) (см²) .
6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.