В треугольник с основание а и высотой с вписан квадрат,причем две вершины квадрата лежат на основании треугольника,а две другие- на его боковых сторонах.Найдите сторону квадрата.
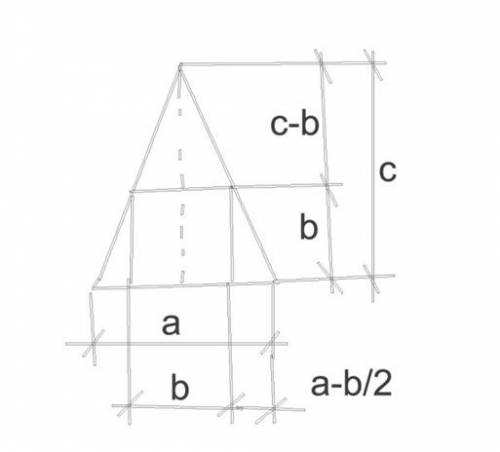
Из подобия треугольников, имеющих параллельные стороны и равные углы, вытекает пропорция, где в -сторона квадрата, с - высота (в условии h)
(с-в)/(в/2) = в / ((а-в)/2) =( 2*(с-в)) / в = (2*в) / (а-в) = ас-ав-св+b^2 = b^2 = -b(a+c)+ac = 0.
Отсюда в = ас/(а+с)
Площадь прямоугольника - произведение длины на ширину.
Диагональ делит прямоугольник на 2 одинаковых прямоугольный треугольника. причем диагональ является гипотенузой этих треугольников, а стороны прямогульника - катеты этих треугольников.
Короче, чтобы посчитать площадь прямоугольника, надо найти длину катетов этих треугольников.
Длина гипотенузы известна, угол CAD между гипотенузой и катетом известен.
Длина катета, противолежащего углу CAD: |CD| = 3 * sin 37 град
Длина катета, прилежащего углу CAD: |AD| = 3 * cos 37 град
Подозрение вызывает величина угла 37 град - это вручную не посчитаешь
У меня получилось 4.325677632 (для 37 град)
Скорее всего, должно быть 30 град.
Тогда легко:
|CD| = 3 * sin 30 град = 3 *1/2 = 3 *1/2
|AD| = 3 * cos 30 град = 3 * (V 3)/2 (здесь значок V означает корень квадратный - не знаю как нарисовать)
Площадь = |CD| * |AD| = 9 * (V 3) /4
Короче, девять четвертых корня из трех = 3.897114317 (для угла 30 град)
номер 1
дано
BD-17см
DC-25см
решение
25-17=18- BC
N2
Дано
х-угол 1
х11- угол 2
решение
х+х11=х12
180/12=15- х
180-15=175-х11
N3
дано
угол1 -35
решение
т.к.
угол вертикальный то
угол на против него равен 35- угол 2
угол 1 и допустим угол3 смежные значит
180-35=145 - угол3
угол 2 и допустим угол4 смежные значит
180-35=145 - угол4
N4
дано
АОС - 43
решение
т.к. ОС биссектриса
следует АОС это половина АОВ
значит
43*2=86- АОВ
Объяснение: