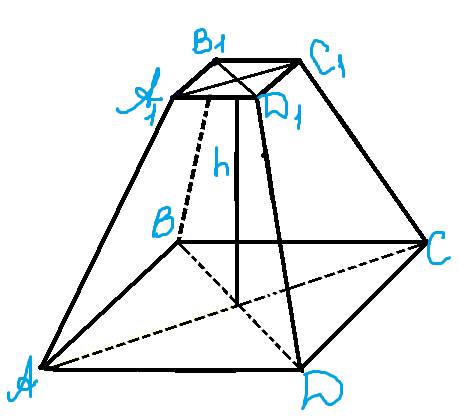
Дано:
A1B1=B1C1=C1D1=A1D1=2(см).
AB=BC=CD=AD=8(см).
S(площадь)сечения=S(AA1C1C)=20(см.квадрат).
Найти:
h(высоту правильной четырёхугольной пирамиды).
Во-первых:
Рассмотрим нижнее основание ABCD.
Теперь по теореме Пифагора найдём диагональ квадрата ABCD:
AC(квадрат)=AD(квадрат)+DC(квадрат);
AC=√8(квадрат)+8(квадрат)
AC=8√2(см).
Во-вторых:
Верхнее основание A1B1C1D1
Теперь опять-же по теореме Пифагора найдём диагональ квадрата:
A1C1(квадрат)=A1D1(квадрат)+D1C1(квадрат);
A1C1=√2(квадрат)+2(квадрат)=2√2(см)
Ну и третье:
Сечение AA1C1C - оно диагонально, выглядит как равнобедренная трапеция.
Площадь трапеции мы уже знаем по формуле:
Sтрап.=a+b/2*h
То есть:
S(сечения)=A1C1+AC/2*h
Теперь подствим всё известное и найдём наконец-то h:
20=2√2+8√2/2*h
40=10√2*h
h=40/10√2=4/√2=4*√2/√2*√2=4√2/2=2√2(см).
h=2√2(см).
Пусть общая высота конуса и пирамиды равна Н.
Обозначим объемы конуса и пирамиды через V1 и V2 соответственно ,
а их боковые поверхности – через S1 и S2
тогда V1=1/3pi*R^3H , S1=pi*RL ,
где L-образующая конуса.
Найдем V2 и S2.
Так как периметр основания пирамиды равен 2р ,
а основание конуса – вписанная в основание пирамиды окружность,
то площадь основания пирамиды равна pR,
откуда V2=1/3pRH, S2=pL (высота любой грани равна L).
Тогда
V1 : V2 =1/3piR^2H : 1/3pRH = pi*R/p
S1 : S2 =pi*RL : pL = pi*R/p
ответ V1 : V2 = S1 : S2 = pi*R/p