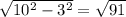. Значит, вся диагональ -- 
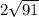, а сторона квадрата, которая в 
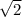раз меньше, чем диагональ, равна 
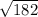. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 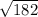. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 
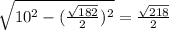, откуда площадь одного треугольника равна 
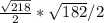, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 
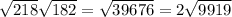Может, обсчитался где-то.
Назовем соприкосновение наклонной и плоскости точкой А, а соприкосновение плоскости с перпендикуляром В. Рассмотрим треугольник MAB, угол M = 60 градусов по условию, угол B = 90 градусов т.к. "перпендикуляр". Третий угол А по теореме о сумме углов треугольника = 180 - 60 - 90 = 30.
Теперь нам известны все углы и одна сторона MB = 20см, остается "решить треугольник".
Т.к. знаем все углы, воспользуемся теоремой Синусов: MB/sinA = AB/sinM = AM/sinB.
Подставим известное: 20/sin30 = AB/sin60 = AM/sin90. Сдесь 2 неизвестных, по условию нам нужно найти длину наклонной AM. Выразим её из равенства:
AM = sin90*20/sin30
AM = 1*20/0.5 = 20*2 = 40 см.
ответ: 40см