Найдите площадь равнобедренной трапеции с основаниями 10 см и 18 см, если её боковая сторона образует с бо'льшим основанием угол в 60°.
=============================================================
Опустим из вершин равнобедренной трапеции высоты ВЕ и СН на основание AD ⇒ BC = EH = 10 см, ЕН = HD = (AD - BC)/2 = (18 - 10)/2 = 8/2 = 4 смРассмотрим ΔАВЕ (∠АЕВ = 90°):tg60° = BE / AE ⇒ BE = AE•tg60° = 4•√3 смВЕ = СН = 4√3 смПлощадь трапеции ABCD:S abcd = (BC + AD)•BE/2 = (10 + 18)•4√3/2 = 28•2√3 = 56√3 см²ОТВЕТ: S abcd = 56√3 см²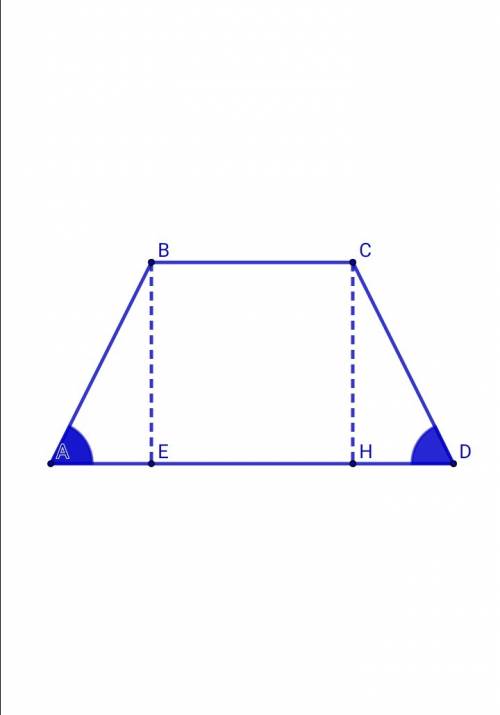
Для решения задачи нужно сделать рисунок.
Углы при основаниях равнобедренной трапеции равны, а биссектрисы равных углов В и С делят их на равные половины.
В треугольниках ВН₁С и ВН₂С с общим основанием ВС углы при основании равны, следовательно, они равнобедренные.
Углы Н₂ВН₁ и Н₂СН₁ состоят из половин смежных углов и поэтому равны 90°
Катеты прямоугольных треугольников Н₂ВН₁ и Н₂СН₁ равны, гипотенуза общая - треугольники равны, и их острые углы при гипотенузе Н₂Н₁ равны.
Поэтому Н₁Н₂ - биссектриса угла ВН₁С и делит его на два по 30°.
Катет ВН₂ противолежит углу 30° и по свойству такого катета равен половине гипотенузы Н₁Н₂ ( или ВН₂=Н₁Н₂•sin30º)
Отрезок ВН₂=12:2=6см
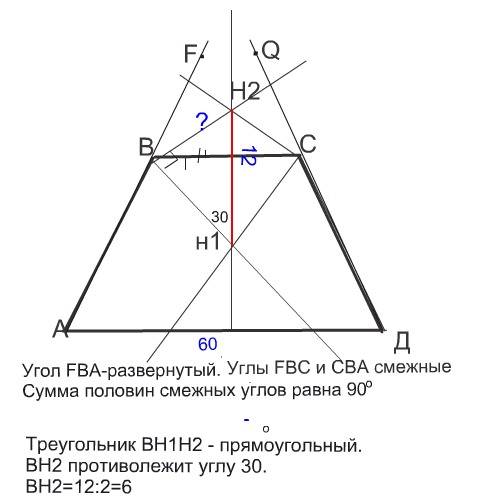
B и C
Объяснение: