ответ: 12√39 (ед. площади)
Объяснение:
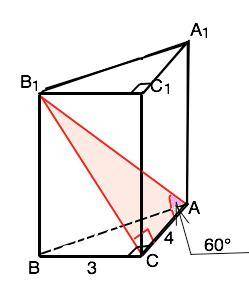
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)
Такие окружности называются ВНЕвписанными, вписанной называется окружность, которая касается всех трех сторон.
Далее, у любого треугольника есть три вневписанных окружности, а заданы радиусы только двух.
Я буду считать, что эти заданные окружности касаются катетов и продолжений другого катета и гипотенузы.
Поскольку каждая из этих окружностей касается сторон прямого угла, то центры их лежат на биссектрисе этих углов (поскольку углы эти вертикальные, у них даже биссектриса - одна :)), только по разные стороны от вершины прямого угла.
Поэтому (этого вполне достаточно) расстояния от вершины прямого угла до центров этих окружностей равны 7√2 и 23√2, а между центрами расстояние 30√2.
Свойство высоты h: h² = 9*16 = 144.
Отсюда h = √144 = 12 дм.
ответ: S = (1/2)*(9 + 16)*12 = 25*6 = 150 дм².