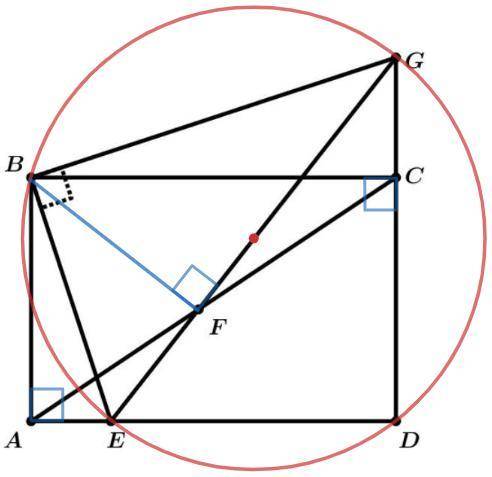
Точки A-F-C лежат на прямой Симсона точки B относительно треугольника EGD.
Объяснение:
Основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на прямой Симсона.
Точка B лежит на описанной окружности треугольника EGD (прямые углы EBG и EDG опираются на диаметр EG).
A и С - основания перпендикуляров из точки B на стороны треугольника EGD.
Тогда AC - прямая Симсона точки B относительно треугольника EGD.
(Прямая Симсона пересекает сторону EG в точке F, следовательно BF⊥EG)
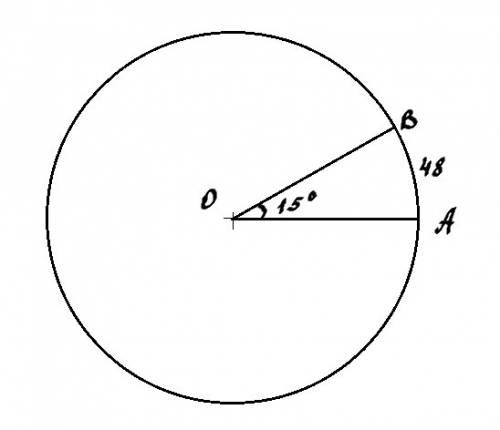
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.
Принадлежит точка (2;7)
Объяснение:
Для того, чтобы это узнать следует вместо у и х подставить данные значения:
у = 6 х - 5
7 = 6 * 2 - 5
7 = 7
Значит точка принадлежит