Дано :
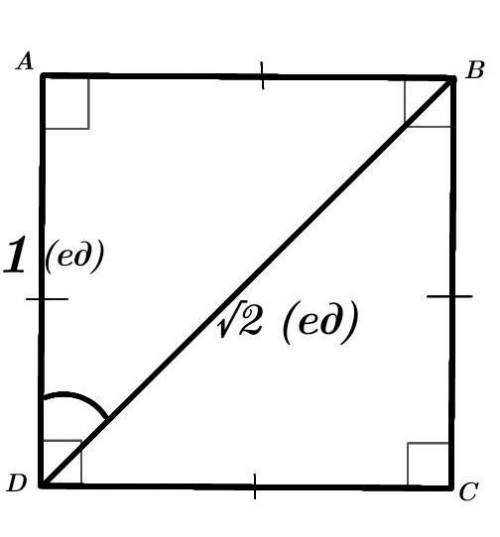
Четырёхугольник ABCD — квадрат.
AD = 1 (ед).
BD — диагональ = √2 (ед).
Найти :
соs(∠BDA) = ?
Квадрат — четырёхугольник, всё стороны которого равны, а все углы прямые.
Рассмотрим прямоугольный ∆ABD.
Косинус острого угла прямоугольного треугольника — отношение прилежащего катета к гипотенузе.
В нашем случае катет, прилежащий к ∠BDA — AD, а гипотенуза — BD (так как лежит против прямого угла).
То есть —
cos(∠BDA) = AD/BD
cos(∠BDA) = 1 (ед) / √2 (ед)
cos(∠BDA) = 1/√2
Или —
cos(∠BDA) = (√2)/2 (одно и тоже).
(√2)/2.
Sбок=1/2 Р *а а -апофема
1) рассмотрим тр-к SCO-прямоугольный, угSCO=30*, SC=4cm => SO=2cm,
по тПифагора CO=2sqrt3
т.к. АН=СМ - высота, медиана, биссектирса АВС, CO=2sqrt3 , то СМ= 3sqrt3
2) рассмотрим АМС-прямоугольный, угАМС=90*, угМСА=30* , СМ= 3sqrt3 ,
то АС=АВ=ВС= 3sqrt3 : sqrt3/2=6см СН=1/2ВС=3см
3) проведем SH -высоту к ВС, это апофема пирамиды
рассмотрим СSH- прямоугольный SC=4cm, НС=3см
по тПифагора SH= sqrt7
4) Sбок=1/2 Р *а
Sбок=1/2 3*6 * sqrt5= 9sqrt7 (во всех случаях sqrt-это корень квадратный)
В равнобедренном треугольнике ABC с основанием ВС проведена высота АF, найдите угол ABF ,если угол А 30 градусов