Геометрия: Определить углы треугольника. (см.картинку

Определить углы треугольника. (см.картинку

👇

Увидеть ответ

Открыть все ответы

Ответ:

Шист

11.05.2021

ответ: 11

Объяснение:

Так как ABCD параллелограмм, то BC || AD ⇒ ордината точки C совпадает с ординатой точки B (равной 8)

Пусть абсцисса точки C равна x, тогда C имеет координаты (x; 8)

По формуле расстояния между точками составим уравнение для A и C:

$AC=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \\ \\ \sqrt{61}=\sqrt{(5-x)^2+(3-8)^2} \\ \\ \sqrt{61}=\sqrt{25-10x+x^2+(-5)^2} \\ \\ 61=50-10x+x^2\\ \\ x^2-10x-11=0\\\\\sqrt{D}=\sqrt{100+44}=12\\\\ x_1=\frac{10-12}{2}=-1\\\\ x_2=\frac{10+12}{2}=11$

Так как ABCD параллелограмм, то BC = AD = 3 ⇒ абсцисса точки B меньше на 3, чем абсцисса точки C. Чтобы ∠ BAD был острым, нужно, чтобы абсцисса точки B была больше абсциссы точки А.

На основе найденных x, найдём абсциссы точки B:

При x = -1: -1 - 3 = -4 < 5 -- угол тупой (не подходит)

При x = 11: 11 - 3 = 8 > 5 -- угол острый

4,4(92 оценок)

Ответ:

тетрадка535243

11.05.2021

Сечения шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144π см, 25π см. Найти площадь поверхности шара, если расстояние между параллельными плоскостями равен 17 см

* * *

Сечение шара плоскостью - круг.

Расстояние между плоскостями равно длине перпендикуляра, опущенного с одной плоскости на другую.

Центр шара и центры сечений параллельными плоскостями лежат на одной прямой.

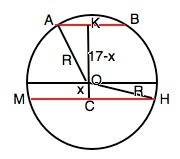
На схематическом рисунке приложения – сечение шара через его центр О и центры сечений.

АК- радиус меньшего сечения, СН - радиус большего сечения, СК - расстояние между центрами сечений, ОА=ОН - радиус шара.

Квадрат радиуса меньшего сечения АК²=S1:π=25

Квадрат радиуса большего сечения СН²=S2:π=144

Обозначим расстояние между центром шара и большим сечением СО=х, тогда между центром шара и меньшим сечением ОК=17-х.

Из ∆ АОК по т.Пифагора

R²=АК²+ОК²

Из СОН