Значит 18 см
1) Чтобы найти координаты вектора AС, зная координаты его начальной точки А и конечной точки С, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. То есть:
AС = (Сx - Ax; Сy - Ay) = (5 - 1; -2 - (-2)) = (4; 0).
Таким же найдем координаты вектора ВА:
BA = (Ax - Bx; Ay - By) = (1 - 3; -2 - 6) = (-2; -8).
Задать вопрос
Войти
АнонимМатематика10 ноября 23:50
Даны точки A(1;-2),B(3;6),C(5;-2), 1)найдите координаты векторов AC,BA,2)найдите координаты точки M, делящей пополам
отрезок BC, найдите длину отрезка AM.
ответ или решение1
Родионова Елена
1) Чтобы найти координаты вектора AС, зная координаты его начальной точки А и конечной точки С, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. То есть:
AС = (Сx - Ax; Сy - Ay) = (5 - 1; -2 - (-2)) = (4; 0).
Таким же найдем координаты вектора ВА:
BA = (Ax - Bx; Ay - By) = (1 - 3; -2 - 6) = (-2; -8).
2) Точка М расположена на отрезке ВС и делит его пополам, следовательно, для поиска координат точки М необходимо определить координаты отрезка ВС и разделить их пополам, то есть:
М = ВС / 2 = (Сx + Bx; Сy + By) / 2 = ((Сx + Bx) / 2; (Сy + By) / 2) = ((5 ++ 6) / 2) = (8 / 2; 4 / 2) = (4; 2).
Для вычисления длины отрезка воспользуемся формулой вычисления расстояния между двумя точками A (xa; ya) и B (xb; yb):
AB = √(( xb - xa)^2 + (yb - ya)^2).
Подставим значения точки А (1; -2) и М (4; 2) в формулу:
AM = √((4 - 1)^2 + (2 - (-2))^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5.
ответ: координаты вектора АС (4; 0), вектора ВА (-2; -8), координаты точки М (4; 2), длина отрезка АМ = 5.
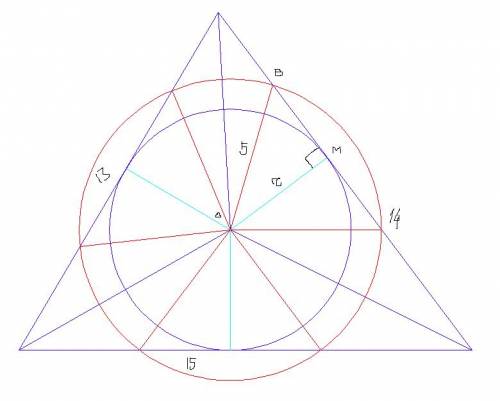
Если радиус окружности R, расстояние до хорды r, длина хорды m, то
(m/2)^2 + r^2 = R^2;
Поскольку центр окружности совпадает с центром вписанной в треугольник окружности, расстояние до искомых хорд будет одинаковым - равным радиусу вписанной окружности. То есть r - это радиус вписанной окружности в треугольник со сторонами 13,14,15.
ПОЛУпериметр этого треугольника равен (13 + 14 + 15)/3 = 21;
Площадь треугольника легко считается по формуле Герона и равна 84.
Этот треугольник составлен из двух Пифагоровых треугольников - со сторонами (9,12,15) и (5,12,13), приставленных друг к другу катетами 12 так, что катеты 9 и 5 вместе образуют сторону 14. Поэтому высота к стороне 14 равна 12, а площадь 12*14/2 = 84.
r = S/p = 84/21 = 4;
откуда
m/2 = 3; (здесь тоже Пифагорова тройка 3,4,5, самая первая)
m = 6; (все хорды одинаковые, само собой)
18
Объяснение:
36:2=18
ответ :18
Ну все