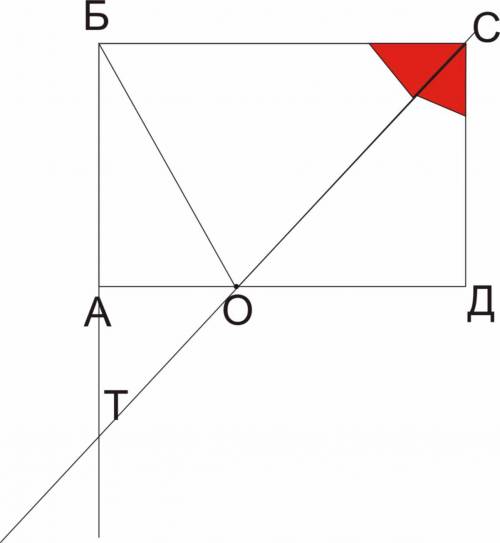
по условию углы БСО = ОСД следовательно они равны по 45 гр. т.к. угол С в прямоугольнике АВСД =90
тр-к ОСД - равнобедренный, т.к. угол ОСД=45 гр., а СДО = 90 гр., следовательно угол СОД=ОСД = 45 гр.
уголы СОД и АОТ - вертикальные - следовательно равны.
ответ: угол АОТ = 45 гр.
или
по условию углы БСО = ОСД следовательно они равны по 45 гр. т.к. угол С в прямоугольнике АВСД =90
углы БСО и СОД равны, как накрест лежащие при параллельных прямых АД и БС
уголы СОД и АОТ - вертикальные - следовательно равны.
ответ: угол АОТ = 45 гр.
Проведем BD параллельно АС. Тогда <PAC=<BDA, как накрест лежащие при параллельных прямых BD и AC и секущей АD.
∆АКМ ~ ∆BKD по двум углам (1).
∆АРС ~ ∆DРВ по двум углам (2).
Из (1) BD/AM=4 и BD=4AM = 2AC.
Из (2) BP/PC=2.
ВМ - медиана и по ее свойствам Sabm=Scbm.
Треугольники АВК и АКМ - треугольники с общей высотой к стороне ВМ. Значит Sabk/Sakm=4/1. => Sabk=Sabc*(1/2)*(4/5)=(2/5)*Sabc.
Sakm=Sabc*1/(2*5)=(1/10)*Sabc.
Треугольники ABP и APC - треугольники с общей высотой к стороне ВC.
Значит Sabp/Sapc=2/1. => Sapc=Sabc*1/3=(1/3)*Sabc.
Тогда Skpcm=Sapc-Sakm = (1/3)*Sabc-(1/10)*Sabc = (7/30)*Sabc.
Sabk/Skpcm=(2/5)/(7/30)=12/7.