Одна из формул площади треугольника S-h•a/2
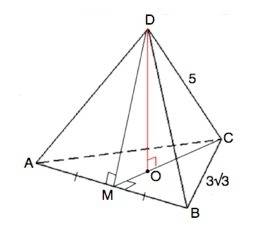
S (MDC)=DO•CM/2 ( DO - высота, СМ - основание треугольника)
∆ АВС правильный, -- все углы равны 60°
Медиана правильного треугольника является его биссектрисой и высотой.
СМ⊥АВ
СМ=СВ•sin60°=3√3•√3/2=4,5
Вершина правильной пирамиды проецируется в центр основания ( для правильного треугольника в основании - точку пересечения медиан)
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
СО=4,5•2/3=3
∆ DCO египетский, ⇒ DO=4
S (MDC)=4•4,5:2=9 см²
Объяснение:
Если один угл равен 60, а второй 90(т.к прямоугольный), то третий будет равен 180-60-90= 30.
Если угол 30 напротив гип. То прилижещая сторона к углу равна 1:2 гипотенузы.
Значит-16.2 надо рвзделить на 3
Так как в гипотенузе 2 катета и +один катет наименьший
16,2:3=5,4- наименьший катет
5, 4 *2 =10 ,8
ответ-10,8