Единичный тетраэдр - треугольная пирамида, длина каждого ребра которой равна единице. Следовательно, пирамида МАВС - правильная, все ее грани - правильные треугольники.
Данное сечение - треугольник, высота которого равна высоте МО пирамиды, а основание - высоте АН основания пирамиды.
Основание О высоты правильной пирамиды - точка пересечения высот ( медиан, биссектрис) основания АВС.
АО=радиусу описанной окружности.
АО=R=a/√3=1/√3 (по формуле радиуса описанной окружности).
По т.Пифагора из ∆ АМО высота
МО=√(AM²-AO²)=√(1-1/3)=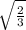
S ∆ MAH= MO•AH:2 =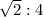
Сумма смежных углов 180 градусов.
2. Треугольник-это геометрическая фигура, образованная тремя лучами, соединяющими три точки, не лежащих на одной прямой.
Построение: сначала строим один из заданных отрезков, а потом от каждой из точек, ограничивающих его, с циркуля откладываем две других стороны. Соединяем эти точки с точкой пересечения дуг.
3.1)МВ=NB(по условию)
2)DB=KB(по условию)
3) угол MBD=углу NBK(как вертикальные), значит треугольники равны по первому признаку равенства треугольников.