Пусть нам известна хотя бы сторона этого шестиугольника:))). Пусть она равна а. Кстати, радиус описанной окружности тоже равен а. Этот шестиугольник состоит из 6 равных треугольников. Достаточно вычислить площадь хотя бы одного. Треугольники будут равносторонними. потому что угол при вершине треугольника, где центр этого шестиугольника, равен 360:6=60. А другие два угла равны между собой как в равнобедренном треугольнике. Значит 180-60=120 градусов - сумма двух одинаковых углов треугольника. 120:2=60 градусов - мера углов при основании треугольника. Площадь равностороннего треугольника со стороной а можно вычислить по формуле, перемножив две одинаковые стороны друг на друга, затем умножив на синус 60 градусов и разделить пополам.
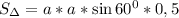
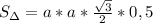
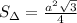
Всего таких треугольников 6. Значит надо умножить на 6.
Получается ответ
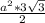
1) 72° (так как сумма углов треугольника равна 180°)
2)49° (так как сумма углов треугольника равна 180°)
3)65° (так как внешний угол смежный с внутренним)
4)3° (так как внешний угол смежный с внутренним)
5)68° (биссектриса делить угол на 2 равных угла)
6)82° (биссектриса делить угол на 2 равных угла)
7) 44° (угол при высоте равен 90°, а сумма ∠Δ равна 180 °, тоесть нужно было от 180 отнять 90 и 46)
8) 8° (угол при высоте равен 90°, а сумма ∠Δ равна 180 °, тоесть нужно было от 180 отнять 90 и 82)
9) 7 (медиана соединяется с центром стороны, тоесть делит сторону AC пополам)
10) 29 (медиана соединяется с центром стороны, тоесть делит сторону AC пополам)
11) 10,5 и 11 (ну если середина то нужно на 2 делить)
12) 33 и 18,5 (ну если середина то нужно на 2 делить)
Т.к. △ABC -- прямоугольный (с прямым углом C) и ∠A = 60°, то ∠B = 90° - 60° = 30°.
В прямоугольном треугольнике напротив угла в 30° лежит катет, равный половине гипотенузы. Из этого AC = AB/2 = (6√3)/2 = 3√3 (см).
ответ: 3√3 см.