1. Укажите координаты вектора, который коллинеарен вектору b(3;2;1)
a)(2;1;0)
б)(1;2;3)
в)(6;9;3)
г)(9;6;3)
2. В треугольнике с вершинами в точках М(-1;2;0) N(0;3;-1) P(2;1;-3) найдите длину медианы МК
а)3
б)2√2
в)√6
г)√7
3. Дано точки А(1;0;-1) В(-1;-2;0) К(2;1;2) Найдите на оси ординат такую точку Р, чтобы векторы КР и АВ были перпендикулярные. В ответ записать только ординату.
4. Какая из точек лежит в плоскости ху?
а)А(1;2;3)
б)В(0;1;2)
в)С(0;0;3)
г)D(1;2;0)
5. Найдите расстояние между точками А(1;1;1) и В(2;2;2)
а)√2
б)1
в)√3
г)√5
6. Найдите абсолютную величину вектора m=-2a+3b, если а(1;-3;0) и b(2;-1;4)
7. Дано точки А(1;0;1) В(-1;1;2) С(0;-1;2) Найдите координаты точки D(x;y;z), если векторы АВ=СD
а)(-2;0;3)
б)(2;3;0)
в)(2;-3;0)
г)(-2;3;0)
8. Найдите значение n, если векторы а(n;-2;1) и b(n;2n;4) перпендикулярные
9. Вычислите косинус угла между векторами а(-1;2;-2) и b(6;3;-6)
а)3/9
б)2/9
в)1/9
г)4/9
10. Дано точки К(0;2;1) Р(2;0;3) Т(-1;у;0) Найти значение у, чтобы выполнялось условие |КТ|=|РТ|
11. Найдите градусную меру угла В треугольника АВС, если известны координаты его вершин А(0;2;-2) В(0;-1;1) С(1;-1;0)
12. Найдите длину средней линии треугольника АВС, которая параллельна стороне АС, если А(2;3;4) В(-1;2;-2) С(5;7;4)
а)4,5
б)2,5
в)5,5
г)3,5
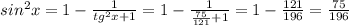
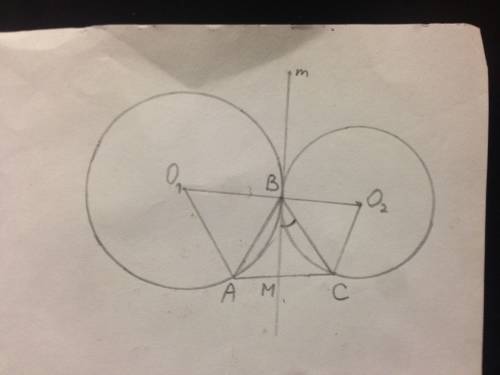
в) Как расположена по отношению к плоскости прямая , параллельная прямой
11? ответ обоснуйте. (1б)
6. Плоскость проходит через основание трапеции . Точки и – середины
боковых сторон трапеции .
а) Докажите, что прямая параллельна плоскости . (1б)
б) Найдите , если = 4, = 6. (1б)
7. Параллелограммы и 11 не лежат в одной плоскости. Докажите
параллельность плоскостей 1 и 1.
( 2б)
8. Дан тетраэдр . ∈ , ∈ , ∈ .
а) Постройте точку пересечения с плоскостью . (1б)
б) Постройте линию пересечения плоскости и плоскости . (1б)
9. Концы двух равных перпендикулярных отрезков и лежат на двух параллельных
плоскостях. а) При каком дополнительном условии пересечения
отрезков является квадратом? (2б) б)
Докажите, что если не является квадратом, то - трапеция, в которой высота
равна средней линии. (2б)
10. Дан куб 1111.Точка - середина ребра 11. Найдите косинус угла между
прямыми и 1. (5б)