Верно ли утверждение: Медиана равнобедренного треугольника является высотой и биссектрисой. Выберите правильный ответ: *

Да
Не всегда
Нет
В равнобедренном треугольнике АВС к основанию треугольника проведена высота ВМ. Градусная мера угла АВМ равна 51°.Найдите градусные меры углов МВС и ВМС. Выберите правильный ответ. *

102° и 51°
51°и 90°
51° и 51°
недостаточно данных для решения
В равнобедренном треугольнике АВС к основанию треугольника проведена высота ВМ.АМ=1,9дм.Найдите длину отрезка АС.(ответ выразите в сантиметрах).Выберите правильный ответ: *

недостаточно данных для решения
19
3,8
38
Периметр равнобедренного треугольника АВС равен 27 см. Найдите длину боковой стороны АВ, если АС = 9 см.Выберите правильный ответ: *

18 см
9 см
5 см
27 см
В равнобедренном треугольнике длина основания равна 16 см. Чему равен периметр треугольника, если боковая сторона на 4 см меньше основания?Выберите правильный ответ: *

40 см
44 см
24 см
36 см
В равнобедренном треугольнике АВС на основании АВ отмечены точки М и К так, что АМ =КВ. Длина отрезка СМ равна 7 дм. Найдите длину отрезка СК.( В ответ укажите только число) *

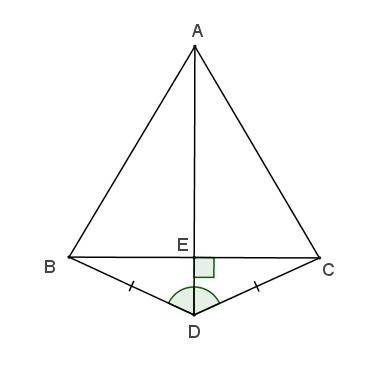
Пользуясь рисунком , выберите верные утверждения: *

Подпись отсутствует
треугольник АВС называется равносторонним
стороны АВ и ВС называются боковыми сторонами
стороны АВ и АС называются боковыми сторонами
сторона АС – основание треугольника АВС
В равнобедренном треугольнике АВС стороны АВ и АС равны. Градусная мера угла В равна 39°. Градусную меру какого угла вы можете найти, по условию задачи? Запишите градусную меру этого угла (в ответ укажите только число) *

👇

Увидеть ответ

Открыть все ответы

Ответ:

GanDyrAS

13.08.2020

216см2

Объяснение:

Центр окружности, описанной около равнобедренной трапеции, который находится на большем основании, делит его на две равные части:

AO=OD=R=1/2×AD=1/2×26=13 см

2. В равнобедренной трапеции AE и FD можно найти, зная основания:

AE=FD=(AD−BC)/2=(26-10)/2=8

Вычисляем EO и OF:

EO=OF=R−AE=13−8=5 см

3. Так как ΔEBO — прямоугольный, то высоту трапеции BE можно найти по теореме Пифагора:

BE=R2−EO2−−−−−−−−√=132−52−−−−−−−√=169−25−−−−−−−√=144−−√=12 см

4. Вычисляем площадь трапеции:

S=AD+BC2×BE=(26+10)/2×12=18×12=216см2

4,7(48 оценок)

Ответ:

markzastawa

13.08.2020

Пусть E - точка пересечения прямых BC и AD. Если Е не совпадает с D (на чертеже изображен как раз один из таких случаев), то прямоугольные треугольники BED и CED равны по гипотенузе и катету:
BD=CD по условию, а ED - общий катет. Отсюда ∠BDE=∠CDE,
а т.к. точки A,D,E лежат на одной прямой, то и ∠BDA=∠CDA.
(Заметим, что если Е совпала с D, то равенство углов ∠BDA и ∠CDA следует сразу из условия, т.к. BC⊥AD).
Далее, треугольники BDA и CDA равны по сторонам и углу между ними
(AD - общая, BD=CD по условию, ∠BDA=∠CDA доказали выше), а значит, AB=AC, что и требовалось.

Дано: ad перпендикулярно bc; bd=cd. докажите,что: ab=ac. решите *