Площадь боковой поверхности равна 756 дм².
Площадь полной поверхности равна 1145 дм².
Объяснение:
Площадь боковой стороны усеченной пирамиды равна площади равнобочной трапеции с основаниями 17 и 10 дм и высотой, равной апофеме 14 дм.
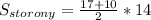
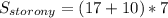
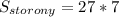
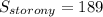 дм².
дм².
В площади боковой стороны таких трапеций четыре.
Значит
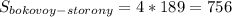 дм².
дм².
Площадь полной поверхности равна сумме площади боковой поверхности и площадей оснований.
Площадь меньшего основания равна площади квадрата со стороной 10 дм
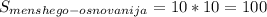 дм².
дм².
Площадь большего основания равна площади квадрата со стороной 17 дм
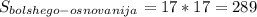 дм².
дм².
Теперь надо сложить все эти три площади
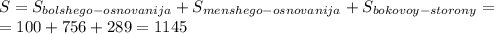
дм².
Длина средней линии трапецыи становит 4+9=13см. Отсюда мы можем найти суму основ трапецыи, за формулой про нахождения средней линии трапецыи (средняя линя равняеться полсуме основ- (ВС+АД)/2=МН), отсюда ВС+АД=13*2=26см.
Расмотрим треугольник АВС, у него: диагональ АС делит среднюю линию на две равных части, отсюда МО-средняя линия этого треугольника, а значит она равна половине линии, которая ей лежит паралельно(линии ВС)=4*2=8см.- это меньшее основание, теперь мы можем найти большее основание: 26-8=18см.
ответ:8см., 18см.