60°
Объяснение:
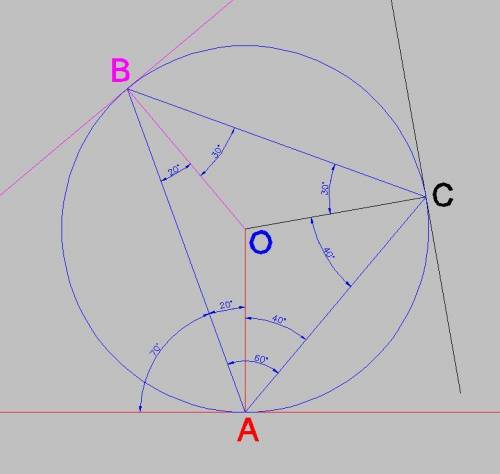
Поставим в центр окружности точку О, и построим из неё радиусы. Построим касательные к окружности в вершинах треугольника.
1. В треугольнике АОВ угол ОАВ = 20°, т.к. по условию угол между хордой АВ и касательной А равне 70°, а угол между радиусом и касательной к нему всегода 90°
2. Треугольник АОВ равнобедренный, углы при основании 20°, угол при вершине
∠АОВ = 180 - 20 -20 = 140°
3. ∠АВС = 50° по условию, значит
∠ОВС = 50 - 20 = 30°
4. Треугольник ОВС равнобедренный, углы при основании 30°, угол при вершине
∠АОВ = 180 - 30 - 30 = 120°
5. Найдём угол при вершине равнобедренного треугольника АОС
∠АОС = 360 - 140 - 120 = 100°
6. Угол при основании ΔАОС
∠ОАС = (180 - 100)/2 = 40°
7. Добрались до финала :)
x = ∠ВАС = 20 + 40 = 60°
В первом задании:
По формуле нахождения длины отрезка получаем:
корень из (16+49)=корень из 55
по формуле нахождения кооржинат середины получаем:
х=(-3+1)/2 х и у—координаты середины
у=(2-5)/2
х=-1
у=-3/2
Во втором задании:
Надо определить величину радиуса R заданной окружности как расстояние между центром М и точкой К.
R = √((-4-1)²+(2+3)²) = √(25+25) = √50 = 5√2.
Уравнение окружности (х-хо)²+(у-уо)² = R².
В данном примере (х-1)²+(у+3)² = 50.
В третем задании: Дано точки К (3; -2) и Р (5; 2).
Найти уравнение прямой
Решение
уравнение
ax+by+c = 0
3a-2b+c = 0
5a+2b+c = 0
a = -c/4
b = c/8
-c/4x + c/8y + c = 0
-2x + y +8 = 0