Контрольная работа по теме: «Смежные и вертикальные углы»
1 вариант
1 Прямые MN и PK пересекаются в точке E. ˂МЕР=151.̊ Найдите
остальные углы, образовавшиеся при пересечении прямых.
2 Найдите смежные углы, если их градусные меры относятся как 13:23.
3 Найдите величину каждого из углов, образовавшихся при пересечении
двух прямых, если сумма двух из них равна 1060
4 Прямые АВ и СD пересекаются в точке О. ОК – биссектриса угла АОD,
< СОК = 103°. Найдите < ВОD.
Контрольная работа по теме: «Смежные и вертикальные углы»
2 вариант
1 Прямые АС и PО пересекаются в точке К. ˂РКА=39.̊ Найдите
остальные углы, образовавшиеся при пересечении прямых.
2 Найдите смежные углы, если их градусные меры относятся как 17:19.
3 Найдите величину каждого из углов, образовавшихся при пересечении
двух прямых, если сумма двух из них равна 540
4 Прямые MN и PK пересекаются в точке E. EC – биссектриса угла
РEN, < СEК = 121°. Найдите < KEM.
Критерии оценивания:
«5» -если верно выполнены 4 задания;
«4»- если верно выполнены любые 3 задания;
«3» - если верно выполнено любые 2 задания.
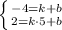
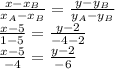
2) ∠BAK = ∠KAC = ∠OCA = ∠OCK, т.к. ∠A = ∠C, и СО и КА — биссектриссы.
В ΔAKB и ΔСОВ: АВ = ВС (т.к. ΔАВС — равнобедренный) ∠BAK = ∠BCO (т.к. АК и СО — биссектриссы равных углов). ∠B — общий. Таким образом, ΔAKB = ΔСОВ по 2-му признаку равенства треугольников.
Откуда AK = СО, что и требовалось доказать.
1) AQ = QB = BF = FC, т.к. AF и CQ — медианы. В ΔAFB и ΔCQB:
АВ = ВС (т.к. ΔАВС — равнобедренный)
QB = BF
∠В — общий. Таким образом, ΔAFB = ΔCQB по 1-му признаку равенства треугольников.
Откуда AF = CQ.
блин хз как рисунок скинуть, я с ноута зашла