MN- средняя линия в треугольнике АВС, параллельная АС, так как М - середина АС, N - середина ВС. По свойству средней линии AB=2MN=2*4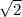
=8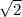
Углы MNC и CMN равны (180-(90+45)=45), углы MNC и АВС равны, как при параллельных прямых MN и АВ и секущей ВС. Углы АВС и САВ равны (180-(90+45)=45).
Если синусы и косинусы не проходили, то возьмем СВ=АВ=Х, тогда по теореме Пифагора:
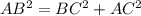
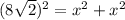
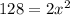
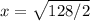
x=8
Тогда АС=ВС=8.
СN=1/2BC=8/2=4, так как N - середина BC, точно так же МС=4.
Из треугольника АСN, где С=90 градусов, CN=4, АС=8, по теореме Пифагора:
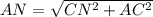
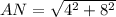
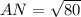
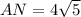
Scmn=CN*MN/2=4*4/2=8
Sabc=AC*BC/2=8*8/2=32
Smabn=Sabc-Scmn=32-8=24.
ответ: АВ=8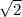, ВС=АС=8, 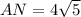, Scmn=8, Smabn=24. ;)
Диагональное сечение прямой призмы - прямоугольник, сторонами которого являются диагонали оснований и боковые ребра.
Площадь диагонального сечения призмы равна произведению диагонали ее основания на высоту ( ребро прямой призмы)
Scечения=dh
Пусть высота данной прямой призмы ( ее боковое ребро) равна х
Тогда меньшая диагональ ромба ( основания призмы) равна 9/х,
а большая диагональ - 12/х
Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам
.
Найдем сторону ромба из прямоугольного треугольника, получившегося при пересечении
диагоналей.
Половины диагоналей - 9/2х и 12/2х
Сторона ромба а, вычисленная по теореме Пифагора, равна
а=√(81/4х²+144/4х²)=7,5/х
Площадь боковой грани прямой призмы равна произведению стороны основания на высоту призмы.
S=х·7,5/х=7,5
Боковых граней 4, площадь боковой поверхности
Sбок=4·7,5=30