Даны вершины: A,(-3, 3) B (7, 5)C (4, 1).
Угол между прямыми АВ и АС можно определить двумя
1) геометрическим по теореме косинусов,
2) векторным через скалярное произведение.
1) Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √104 ≈ 10,19804.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √25 = 5.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √53 ≈ 7,28011.
cos A= АВ²+АС²-ВС² = 0,88897.
2*АВ*АС
A = 0,475695219 радиан,
A = 27,25532837 градусов .
2) х у Длина
Вектор АВ 10 2 10,19804.
Вектор АС 7 -2 7,28011.
Угол определяем по формуле:
α = arc cos |ax*bx+ay*by|/(√(ax^2+ay^2)*√(bx^2+bу^2)).
α = arc cos |10*7+2*(-2)|/(√104*√53) = 66/2√1378 = 33/√1378 ≈
33/37,12142239 ≈ 0,88897.
Угол дан выше.
.
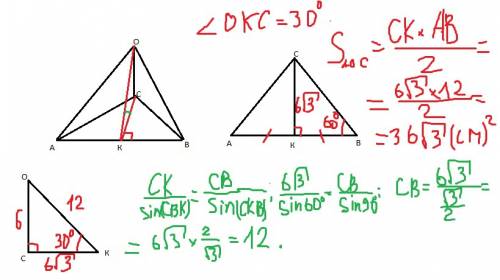
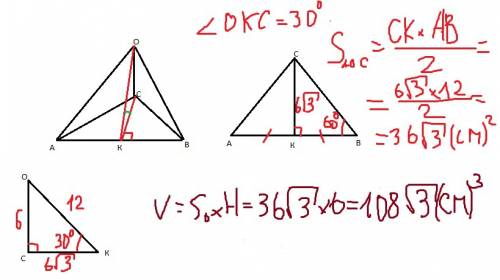
Ясно, что в этом прямоугольном треугольнике есть не только угол в 60°, но и в 30°, т.к. в сумме острые углы составляют 90°. А против острого угла в 30° лежит катет, равный половине гипотенузы, т.е. 6 см. Тогда другой катет равен √(12²-6²)=6√3,
А в маленьком треугольнике, на которые разбивает высота исходный треугольник, тоже есть угол в 30°, против него лежит проекция катета в 6 см для исходного треугольника, для маленького же треугольника сторона в 6 см является гипотенузой, значит, эта проекция равна 3см, и 12-3=9/см/- больший из отрезков, на которые высота, проведенная к гипотенузе разбивает эту гипотенузу.
ответ 9 см