Объяснение:
Все высоты находим по теореме Пифагора
Первый треугольник:
Высота к стороне Б равна: √(17²-8²)=√225=15
Высота к боковой стороне равна: (2√(p(p-a)(p-b)²)/b=(2√(25х9х64))/17=(2х5х3х8)/17=240/17=14.12см
p - полупериметр, равен (17+17+16)/2=25
а - основание
б - боковая сторона
ответ: 15 и 14.12см
Вторая задача:
По формуле h=(2√(p(p-a)(p-b)(p-c)))/a
p - полупериметр, равен 40
ha=(2√(40x10x6x24))30=480/30=16
hb=(2√(40x10x6x24))34=480/34=240/17=14.12
hc=(2√(40x10x6x24))16=480/16=30
ответ, 16, 30 и 14.12см
Дано:
ABCDEFGH - прямоугольный параллелепипед
AB:BC:BF = 1:2:3
Sполн = 550 см²
------------------------------------------------------------------------------
Найти:
AB - ?, BC - ?, BF - ?
Пусть AB = x см, тогда BC = 2x см, и BF = 3x см.
Запишем формулу площади полной поверхности параллелепипеда:
Sполн =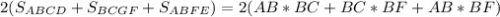
Именно по такой формуле площади полной поверхности параллелепипеда мы найдем все длины параллелепипеда:
Sполн = 2(AB×BC+BC×BF+AB×BF)
550 = 2(x × 2x + 2x × 3x + x × 3x см)
550 = 2(2x² + 6x² + 3x²)
550 = 2×11x²
550 = 22x²
x² = 25
x = √25
x = 5 см ⇒ AB = 5 см, следовательно:
BC = 2x = 2×5 см = 10 см
BF = 3x = 3×5 см = 15 см
ответ: AB = 5 см, BC = 10 см, BF = 15 см
P.S. Рисунок показан внизу↓