Задача 1.
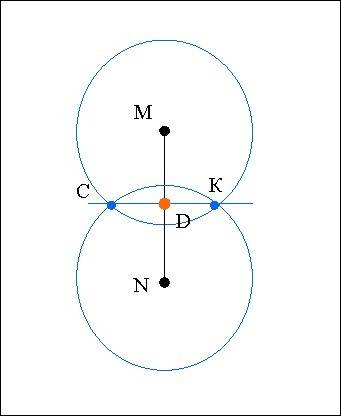
1.Строишь отрезок MN.
2. Ставишь ножку циркуля в точку M - это центр окружности, а радиус должен быть меньше самого отрезка и больше половины отрезка, и строишь окружность.
3. Точно также ставишь ножку циркуля в точку N - это центр окружности, а радиус равен радиусу первой окружности, и строишь окружность.
4.Эти окружности пересекутся в двух точках С и К. Проводишь линию, которая соединяет эти точки.
Эта линия СК пересечет данный отрезок MN в точке D.
Точка D - это и есть середина отрезка MN.
Задача 2 решается также, только там три отрезка и для каждого нужно найти середину. А затем эту серединную точку соединяешь с противоположной вершиной треугольника, это и есть медиана.
Объяснение:
Треугольник , у которого один угол прямой, а два других острые.
Гипотенуза.
Если острый угол прямоугольного треугольника равен 30°, то катет,лежащий напротив него равен половине гипотенузы.
№4
угол BAС=180-(90+42)=48 градусов.
№5
АВ=ВС*2=12*2=24см
№6
Бокова сторона АС является гипотенузой треугольника АСД. Катет СД равен половине гипотенузы. СД=АС:2=7:2=3,5 см.Поэтому угол САД= 30°. Угол АСВ= 180°-(90°+30°)=60°,Угол АСВ=СВА=60°,значит и угол САВ=60°
ответ: в равнобедренном треугольнике АВС все углы равны 60°
№7
Высота ,проведенная на гипотенузу равнобедренного прямоугольного треугольника является медианой и делит его ещё на два равнобедренных прямоугольных треугольника .В получившихся треугольниках эта высота становится катетом. 18:2= 9см,значит и высота ,проведенная на гипотенузу равнобедренного прямоугольного треугольника равна 9 см.