От всех сторон треугольника равноудалена точка пересечения его биссектрис, т.е. центр вписанной окружности.
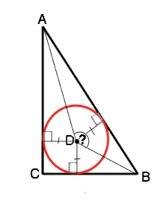
Вершиной угла, под которым видна гипотенуза ( она - длинная сторона прямоугольного треугольника), является центр вписанной окружности, а его величина - разность между суммой углов треугольника и полусуммой его острых углов
∠АDВ=180°-0,5•(38°+52°)=135°
Заметим, что тупой угол, образованный биссектрисами острых углов прямоугольного треугольника всегда равен 135°, так как их сумма 90°, а полусумма -– 45°
есть формула нахождения медианы по сторонам треугольника: медиана к стороне "с" =квадр.корень из ((2*а^2+2*b^2-c^2)/4). Подставляем наши величины (сторона "с" у нас = СК = 4). Корень из ((2*8^2+2*6^2-4^2)/4)=корень из 46. ответ: медиана ДМ=квадратному корню из 46.