По условию секущая плоскость параллельна плоскости КМТ.
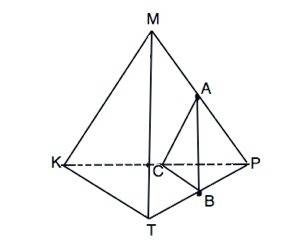
Точки А и В лежат в плоскости грани МРТ и являются серединами сторон МР и ТР треугольника МТР.
Следваоетльно, прямая АВ параллельна МТ.
Из т.В проведем прямую ВС параллельно КТ.
ВС - средняя линия ∆ КТР.
С- середина КР, АС - средняя линия ∆ МКР и параллельна МК.
Две пересекающиеся прямые АВ и МС плоскости АВС параллельны двум пересекающимся прямым МТ и ТК плоскости МКТ. Это признак параллельности плоскостей, следовательно, АВС - искомое сечение.
Половина основания b/2=а*cos(30)=a*sqr(3)/2, b=a*sqr(3)
Известно, что:
R=a^2/sqr(4a^2-b^2)
Подставив значение b, получим: R=a
Отсюда: АВ=2 см
Во второй задаче центр вписанной окружности совпадает с точкой пересечения биссектрис, поскольку радиусы опущенные из центра в точки М, Т и Р, образуют пары равных прямоугольных треугольников (ВОМ и ВОТ и т.д.). Четырехугольник РОТС является квадратом, так как радиусы проведены в точки касания и перпендикулярны катетам. По условия диагональ этого квадрата равна корень из 8, следовательно сторона будет в корень из двух раз меньше, отсюда:
r=sqr(8/2)=2 Угол ТОР=90 град. Угол ТМР является вписанным, он измеряется половиной дуги, на которую опирается. Дуга составляет 90 градусов, так как ограничена точками Р и Т, а угол РСТ прямой. Следовательно угол ТМР=45 град.