ответ: 12 (ед. длины)
Объяснение:
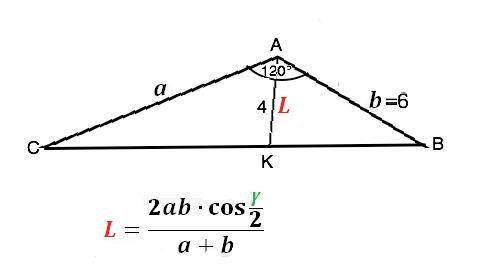
Одна из формул биссектрисы треугольника
L={2ab•cos(0,5γ)}:(a+b) ,
где L биссектриса, а и b- стороны, γ - угол между ними.
На приведенном рисунке АК - биссектриса ∆ АВС, АС=а, АВ=6, угол А=γ =120°
cos0,5γ=cos60°=1/2
4=2a•6•0,5/(a+6) =>
4a+24=6a =>
АС=a=12 (ед. длины)
Или с тем же результатом найти:
1) По т. косинусов из ∆ АКВ найти КВ
2) по т. синусов из ∆ АКВ угол В
3) из суммы углов треугольника угол С
4) по т. синусов вычислить длину искомой стороны АС
Пусть данная пирамида МАВС, МО - высота, точка О - центр треугольника; угол ОМА=45°
МО⊥плоскости основания, ∆ МОА - прямоугольный.
Сумма острых углов прямоугольного треугольника 90°, ⇒∠МАО=45°,
∆ АОМ - равнобедренный. АО=МО=12 см.
О - точка пересечения медиан ∆ АВС, и по свойству медианы АО:НО=2:1. Тогда высота основания АН=12:2•3=18 см
АС=АН:sin 60°=18:√3/2=36:√3•2=12√3
V=S•h:3
Формула площади правильного треугольника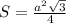 
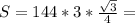36•3•√3 см²
V=36•3•√3•12:3=432√3 см³
* * *
Объём цилиндра равен произведению площади основания на высоту. Пусть основание вписанной призмы – ∆ АВС, АВ - гипотенуза, АС =m, угол АВС=f.
.Центр окружности, описанной вокруг прямоугольного треугольника, лежит в середине гипотенузы, а радиус равен её половине.
⇒ радиус основания цилиндра равен половине АВ.
АВ=m:sin f
R=0,5m:sin f
V=πr²•h
Объяснение:
1) Через любую точку пространства можно провести прямую, параллельную другой прямой, но при этом только одну. Данная тема называется параллельность прямых и плоскостей в пространстве.
2) Две плоскости называются параллельными, если они не пересекаются, то есть не имеют общих точек
3) 1°. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.2°. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны
4) Признак параллельности прямой и плоскости:
Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в плоскости, то эта прямая параллельна и самой плоскости.
1. Проведем произвольную прямую b, лежащую в плоскости α.
2. Через прямую b и точку М проведем плоскость β.
3. В плоскости β через точку М проведем прямую а, параллельную прямой b.
Прямая а будет параллельна плоскости α по признаку параллельности прямой и плоскости.