Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P.
Какой величины∡ N и ∡ K, если ∡ L = 35° и ∡ M = 55°?
1. Отрезки делятся пополам, значит, KP = , = LP,
∡ = ∡ MPL, так как прямые перпендикулярны и оба угла равны °.
По первому признаку равенства треугольник KPN равен треугольнику MPL.
2. В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие ∡ и ∡ M, ∡ и∡ L.
∡ K = °;
∡8
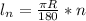 , где n - градусная мера соответственного центрального угла.
, где n - градусная мера соответственного центрального угла.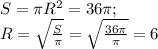 , где S - площадь круга.
, где S - площадь круга.
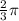 см.
см.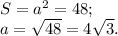
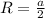 , где a - сторона квадрата.
, где a - сторона квадрата.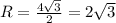
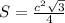 , где c - сторона правильного треугольника.
, где c - сторона правильного треугольника.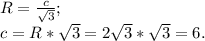
 .
.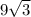 см.
см.
y = 96, P = 196 - дано в условии, найдем x
2X=P-y
x= (P-y)/2
x=50
итого: x = 50, y = 96
нам не хватает высоты, для нахождения площади.
Проведем высоту и рассмотрим половинку этого равнобедренного треугольника, где гипотенуза - x, а прилежащий катет - y/2 (т.к высота в равнобедренном треугольника - медиана)
по теореме Пифагора
h = √(x^2 - (y/2)^2)
h = √(50^2 - 48^2) = √196 = 14
Площадь треугольника: половина основания на высоту, основание - y, высота - h
тогда: S=1/2*hy = 96*14/2 = 672.
ответ: 672