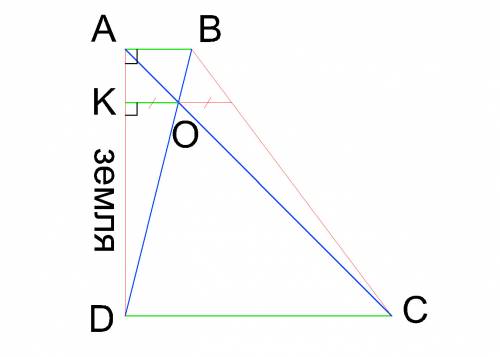
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
1.какие прямые называются параллельными?
1.какие прямые называются параллельными?2.пересекаются ли параллельные прямые?
1.какие прямые называются параллельными?2.пересекаются ли параллельные прямые?3.как называются углы при пересечении параллельных прямых секущей?
1.какие прямые называются параллельными?2.пересекаются ли параллельные прямые?3.как называются углы при пересечении параллельных прямых секущей?4.сколько можно ,через точку не лежащую на прямой ,провести параллельных данной?
1.какие прямые называются параллельными?2.пересекаются ли параллельные прямые?3.как называются углы при пересечении параллельных прямых секущей?4.сколько можно ,через точку не лежащую на прямой ,провести параллельных данной?5.как можно доказать параллельность прямых?