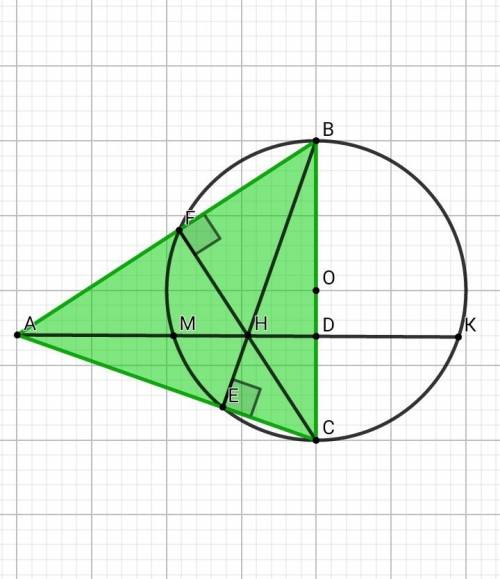
На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 32, MD = 8, H — точка пересечения высот треугольника ABC. Найдите AH.
Решение.
Проведём построения и введём обозначения как указано на рисунке. Угол — вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка пересечения прямых и — точка пересечения высот Продолжим высоту до пересечения с окружностью в точке Получаем, что По теореме о секущих получаем, что Треугольники и — прямоугольные, угол — общий, следовательно, эти треугольники подобны, откуда:
ответ: 30.
Формула диагонали квадрата - а√2, значит,
сторона основания равна 4 дм.
Площадь одной грани призмы 16:4=4.
Поэтому ее высота равна
Н= 4:4=1 дм.
Зная высоту и длину стороны боковой грани, находим ее диагональ:
d²=4²+1²=17
d=√17
Высоту получившегося равнобедренного треугольника
со сторонами √17 и основанием, равным диагонали квадрата (основания) 4√2
найдем из половины этого треугольника:
Эта половина - прямоугольный треугольник с гипотенузой √17 и основанием 2√2
h²=( √17)² - (2√2)²=17-8=9
h= √9=3 дм
Площадь сечения
S=(3*4√2):2=6√2 дм²