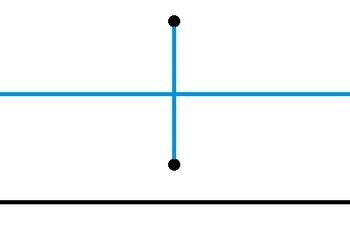
Множество точек равноудаленных от концов отрезка (от двух данных точек) - серединный перпендикуляр к отрезку.
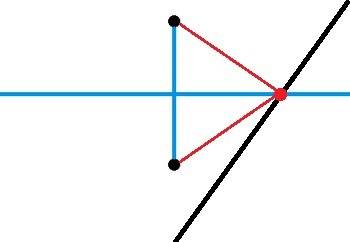
Данная прямая может
1) пересекать серединный перпендикуляр - единственное решение (точка)
2) совпадать с ним - бесконечно много решений
3) быть параллельной ему - нет решений
--------------------------------
Чтобы построить серединный перпендикуляр к отрезку AB, проведем окружности с центрами A и B радиусом AB. Точки пересечения окружностей равноудалены от A и B, следовательно лежат на серединном перпендикуляре к отрезку AB.
1.
а) Ненулевые векторы t и p называются противоположно направленными, если они лежат либо на одной прямой, либо на параллельных прямых и направлены в противоположные стороны.
б) вектор а равен вектору -b, если длины их равны (|а|=|-b| и вектора противоположно направлены (а⇅b)
в) Векторы с и k*c сонаправлены, если k>0.
г) Если АВСД ромб, то сумма векторов СВ и СD равна вектору СА (смотри рис. 1)
2.
а) Верно.
б) Неверно, т.к. средняя линия трапеции соединяет середины боковых сторон.
в) Верно.
3. б) 4√2 (смотри решение на рис. 2).
4. в) вектор DС (смотри решение на рис. 3).
5. Смотри решение на рис. 4.