Объяснение:
Дано: параллелограмм Abcd
Bc=ad и ab=cd
угол b(3)=d(4) и угол a(1)=c(2)
Ac b Bd -диагонали
Пусть точка пересечения О
Док-ть: треугольник воа=соd и вос=аоd
Док-во:
1. Тк диагонали параллелограмма точкой пересечения делятся пополам. (2ое свойство), то треугольники аво и соd равны по стороне и двум прилежащим углам ( ав=сd как противоположные стороны параллелограмма, угол 1=2 и угол 3=4 как накрест лежащие углы при пересечении параллельных прямых ав и сd секущими ас и вd соответственно).
Следует ов=оd и ао=ос.
2. По аналогии:)
Удачи, я старалась. В теореме всё расписано, посмотри и постарайся понять) я верю в тебя!
Первое решение полное и понятное. Если не помните формулу Герона, есть
Вариант решения ( без формулы Герона).
Формула радиуса описанной окружности
R=a•b•c/4S, где а, b, и с - стороны треугольника
S-a•h
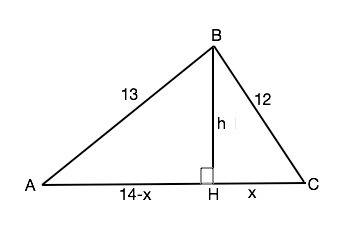
Проведем к большей стороне АС высоту ВН.
Примем СН=х
Тогда АН=14-х
По т.Пифагора
ВН²=АВ²-АН² =169-196+28х-х²
ВН²=ВС²-СН²=144-х²
Приравняем значения квадрата высоты:
169-196+28х-х²=144-х², откуда
28х=171
х=6,107
ВН=√(144-37,3)=√106,7=10,33
S=10,33•14/2=72,31
R=12•13•14/4•72,31=546/72,3= ≈7,55 см
sinA=BH/АВ==10,33/13= ≈0,7946
∠А≈52°36'
Строим острый угол В. Из вершины угла проводим окружность радиусом равным катету, и отмечаем точку пересечения А. Так как треугольник — прямоугольный, то восстанавливаем перпендикуляр из точки А. Полученная точка пересечения С. Соединяем попарно вершины треугольника. Искомый треугольник построен.