Аксиома - это утверждение о свойствах геом.фигур, принимаемое без доказательства. Например: через любые две точки можно провести прямую и при том только одну.
Теорема - это утверждение, требующее доказательства. Например: теорема Пифагора - квадрат гипотенузы равен сумме квадратов катетов.
Обратная теорема - это утверждение, в котором условие исходной теоремы (прямого утверждения) поставлено заключением, а заключение — условием. Например: теорема - если два угла смежные, их сумма равна 180 градусов, а обратная ей - если сумма двух углов равна 180 градусов, то эти углы смежные.
аксиома-утверждение,которое принимается без доказательства
Объяснение:
теорема-утверждение,которое доказывает с определений,аксиом,ранее доказынных теорем
Обратная теорема — это утверждение, в котором условие исходной теоремы поставлено заключением, а заключение — условием.
аксиома параллельных прямых-через точку не лежащую на данной прямой,проходит только одна прямая,параллельна данной
теорема- сумма всех углов треугольника равна 180 градусов
обратная теорема (обратна теореме у равнобедренного треугольника углы при основании равны)
если в треугольнике углы при основании равны, то этот треугольник равнобедренный
ответ: КК1 = 12 см
Объяснение: Исправим условие
Отрезок MN не пересекает плоскость а. Точка К принадлежит
отрезку MN. Через точки M, и N проведены параллельные
прямые, пересекающие плоскость а в точках М1, K1, и N 1
соответственно. Найдите длину отрезка КК1, если MM1 = 6 см,
NN1 = 21 см и МК: KN = 2:3.
Теперь решим.
Для начала проведем параллельно плоскости прямую МН. тогда Поучится треугольник MNH сторона NH которого 6 см,
а МК:КN = 2:3. Треугольники МКЕ и МNH подобные, так как угол М общий, а углы МКЕ и MNH равны как соответственные.
Тогда MN = 5х, а МК = 2х
МН:КЕ = 5х:2х=5:2, значит КЕ =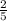
МН =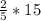 
= 6 с м
Итак, отрезок КЕ = 6 см
КК1 = КЕ+ЕК1 = 6+6=12 см
КК1 = 12 см