Объяснение:
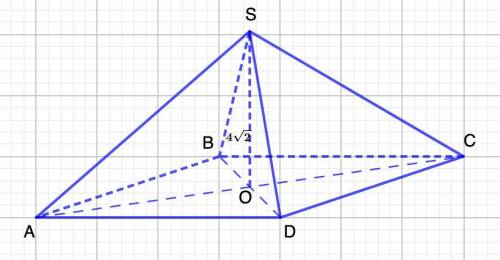
Дано: SABCD - правильная четырехугольная пирамида.
Боковые грани – правильные треугольники.
ABCD - квадрат.
SO = 4√2 см.
Найти: S полн.
По условию все ребра пирамиды равны.
1. Рассмотрим ΔACD - прямоугольный.
Пусть AD = DC = а
По теореме Пифагора:
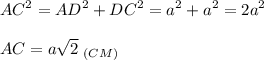
⇒ 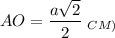
2. Рассмотрим ΔAOS - прямоугольный.
По теореме Пифагора:
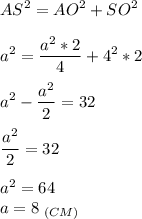
3. S полн. = S осн. +S бок.
S бок. равна площади четырех равносторонних треугольников.
Площадь равностороннего треугольника найдем по формуле:
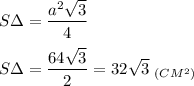
⇒ S бок. = 32√3 * 4 = 128√3 (см²)
Площадь основания:
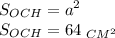
Площадь полной поверхности:
S полн. = (128√3 + 64) см²
R=1/2AB (гипотенуза) => AB=15
r=(AC+BC-AB)/2 => AC+BC=21
возведем в квадрат обе части AC^2+BC^2+2*AC*BC=441
AC^2+BC^2=AB^2=225
AC*BC=2S(площадь)
Подставив получим 225+4S=441 => S=54