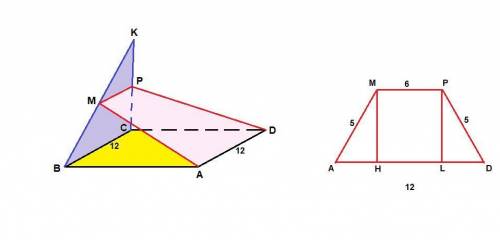
1) MPDA - равнобедренная трапеция
2) 36 см²
Объяснение:
1) МР - средняя линия треугольника ВСК, поэтому
МР║ВС и МР = 1/2 ВС = 6 см
МР║ВС, ВС║AD, ⇒ МР║AD.
Значит, MPDA трапеция. А так как МА = PD = 5 см, то
MPDA - равнобедренная трапеция.
2) Проведем высоты трапеции МН и PL. MPLH - прямоугольник, так как у него все углы прямые, тогда
HL = MP = 6 см.
ΔАМН = ΔDPL по гипотенузе и катету (∠АНМ = ∠DLP = 90°, так как проведены высоты, АМ = DP по условию и МН = PL как высоты), значит
АН = DL = (AD - HL)/2 = (12 - 6)/2 = 3 см
ΔАМН: прямоугольный, египетский, значит МН = 4 см.
Smpda = (MP + AD)/2 · MH = (6 + 12)/2 · 4 = 36 см²
Объяснение: 1) ∆ABD=∆ACD по двум сторонам и углу между ними, АВ=АС, <1=<2 по условию, АD общая. Если треугольник и равны, значит <АВD=<ACD=38°, <ADB=<ADC=102° 2) ∆MNE=∆KNF по двум сторонам и углу между ними, MN=NK, EN=NF, углолENM=углуKNF вертикальные. Отсюда ME=KF=8cm., MN=MK÷2=5cm. 3) ∆ABE=∆DCE по двум углам и стороне между ними, AE=ED, <A=<D, <AEB=<CED вертикальные. Отсюда DE=AE=4cm., DC=AB=3cm., EB=EC=5cm. 4) ∆ABC=∆ADC по трём сторонам, AB=AD, BC=DC, AC общая. Значит <BAC=<CAD, отсюда АС биссектриса.