Дано:
∠A=∠A1
AB=A1B1
AC=A1C1
Доказать:
ΔABC=ΔA1B1C1
Доказательство:
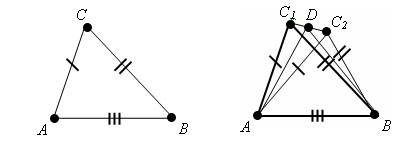
Так как ∠А=∠А1 ( по условию), то треугольник АВС можно наложить на треугольник А1В1С1, так что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона - АС состороной А1С1; в частности совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, ∆АВС и ∆А1В1С1 полностью совместятся, значит они равны. как то такв середине треугольник не нужен
расстояние от точки до плоскости ромба 8см
Объяснение:
площадь ромба через синус любого угла
S=a²×sinα , отсюда сторона
а=√S/sinα= √(144√2÷sin45°)=√(144√2÷√2/2)=
√(144√2×2/√2)=√144×2=12√2 см
радиус вписанной окружности в ромб
r=S/2a=144√2 /2×12√2=144√2/24√2=144/24=6см
точка находится перпендикулярно к оси пересечения диагоналей ромба, и образует прямоугольный треугольник относительно к оси пересечения диагоналей и одной стороны ромба. где расстояние от точки до стороны ромба является гипотенузой, а радиус вписанной окружности катетом . а неизвестное расстояние от точки до плоскости ромба высотой и вторым катетом.
по теореме Пифагора a²+b²=c²
катет a=r=6см радиус вписанной окружности в ромб,
гипотенуза с=L=10см расстояние от точки до стороны ромба ,
катет b=h высота, расстояние от точки до плоскости ромба ,
находим h=√(L²-r²)=√(10²-6²)=√(100-36)=√64=8см