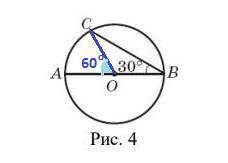
Если диаметр окружности с центром в точке О образует с хордой ВС угол 30°, то
А. треугольник СОВ - равносторонний - НЕ ВЕРНО
В равностороннем треугольнике все углы по 60°, а в треугольнике СОВ ∠В=30°.
Б. ∠ОСВ = 30° - ВЕРНО
В треугольнике СОВ равны две стороны : ОВ=ОС - это радиусы окружности. Значит, ΔСОВ равнобедренный. В равнобедренном треугольнике углы при основании равны : ∠ОСВ=∠В=30°
В. ∠СОА = 50° - НЕ ВЕРНО
∠СОА - внешний угол треугольника ОСВ равен сумме двух внутренних углов, не смежных с ним :
∠СОА = ∠ОСВ + ∠В = 30° + 30° = 60°
ответ : Б, ∠ОСВ = 30°
↑АС = ↑р = ↑а + ↑b
↑DB = ↑q = ↑a - ↑b
Чтобы найти угол между векторами p и q, построим вектор, равный вектору q, с началом в точке А.
∠ЕАС - искомый.
Из ΔABD найдем длину вектора q по теореме косинусов:
|↑q|² = AB² + AD² - 2·AB·AD·cos60° = 25 + 64 - 2·5·8·1/2 = 89 - 40 = 49
|↑q| = 7
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, значит ∠АВС = 120°.
Из ΔABС найдем длину вектора р по теореме косинусов:
|↑p|² = AB² + BC² - 2·AB·BC·cos120° = 25 + 64 + 2·5·8·1/2 = 89 + 40 = 129
|↑p| = √129
Из ΔЕАС по теореме косинусов:
cos α = (AE² + AC² - EC²) / (2 · AE · AC)
cos α = (49 + 129 - 256) / (2 · 7 · √129) = - 78 / (14√129) = - 39√129 / 903
cos α = - 13√129/301