Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
Подробнее - на -
Объяснение:
Основное тригонометрическое тождество:
sinα^2 +cosα^2 =1
Следовательно
sinα =+-√(1-cosα^2)
Синус угла от 0 до 180 - положительный
sinα =√(1 -9/10) =√(1/10)
tgα =sinα/cosα =1/√10 : 3/√10 =1/3
Или (то же самое)
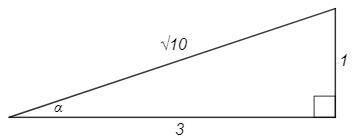
Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета (b) к гипотенузе (c).
Тангенс острого угла в прямоугольном треугольнике - отношение противолежащего катета (a) к прилежащему (b).
cosα=3/√10 =b/c
Пусть b=3, c=√10
По теореме Пифагора
a^2 +b^2 =c^2 => a =√(c^2 -b^2) =√(10-9) =1
tgα =a/b =1/3
20, 45, 115
Объяснение:
Раз дан треугольник с 90 градусов, значит рисуем прямоугольный треугольник. Второй его угол равен 70. Находим третий. 180 - 90- 70= 20.
Далее чертим CD, которая делит угол C поровну. 90:2 = 45. В полученном треугольнике BCD мы знаем уже два угла. BCD = 45 и CBD = 20. Находим третий. 180- 45-20 =115.