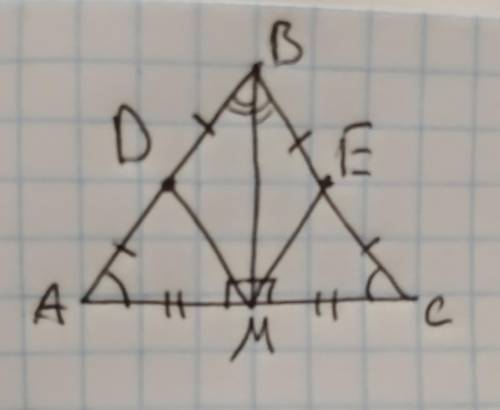
Дано: АВС - рівнобедренний трикутник. ВМ - висота. D i E - середини АВ і ВС.
Довести: <DMB=<MBE
Доведення:
Розглянемо трикутники DMB i MBE
Висота в рівнобедренному трикутнику, проведена до основи, є одночасно бісектрисою і медіаною.
Тому
1) <АВМ=<СВМ.
(За умовою АВ=ВС, точки D i E ділять сторони навпіл, тобто AD=DB=BE=EC.)
2) DB=BE.
3) BM - спільна сторона.
Отже трикутники DMB i MBE рівні за першою ознакою рівності трикутників (дві сторони і кут між ними).
Оскільки трикутники рівні, то і всі їх кути рівні.
Доведено.
а) 2√3 б) 6.
Объяснение:
Условие задачи.
Сторона AB, равная 8, правильного треугольника ABC лежит в плоскости альфа, а длины проекций двух других его сторон на эту плоскость равны 2√7. Найдите: а) длину проекций медианы CK данного треугольника на плоскость альфа; б) расстояние от точки C до плоскости альфа
Решение.
1) Так как ΔАВС - правильный, то АВ = ВС = АС = 8.
2) В правильном треугольнике АВС его медиана СК является высотой, соответственно и в проекции АВС₁ треугольника АВС на плоскость α проекция С₁K медианы СК является и медианой, и высотой равнобедренного ΔАВС₁ со сторонами: АВ = 8, ВС₁ = АС₁ = 2√7.
3) В прямоугольном ΔАКС₁ сторона АС₁ является гипотенузой, а стороны АК и КС₁ являются катетами, при этом АК = АВ/2 = 8/2 = 4.
По теореме Пифагора находим длину проекции медианы:
С₁K = √ ((АС₁)²-(АК)²) = √ ((2√7)²-(4)²) = √ (4*7 - 16) = √12 = 2√3
Таким образом, длина проекции медианы CK данного треугольника на плоскость α = 2√3
4) В прямоугольном ΔАСС₁, образованном стороной АС треугольника АВС, её проекцией АС₁ на плоскость α, а также перпендикуляром СС₁, опущенным из точки С на плоскость α и являющимся кратчайшим расстоянием от точки С до плоскости α, сторона АС является гипотенузой треугольника АСС₁, а стороны АС₁ и СС₁ - его катетами. ПО теореме Пифагора находим СС₁:
СС₁ = √ ((АС)²-(АС₁)²) = √ ((8)²-(2√7)²) = √ (64 - 4*7) = √36 = 6.
Таким образом, расстояние от точки C до плоскости альфа равно 6.
ответ: а) длина проекции медианы CK данного треугольника на плоскость альфа равна 2√3; б) расстояние от точки C до плоскости альфа равно 6.
1. Из прямоугольного треугольника ABD по теореме Пифагора:
BD = √(AB² - AD²) = √(20² - 12²) = √(400 - 144) = √256 = 16 см
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота делит гипотенузу:
AD² = BD · DC
DC = AD² / BD = 144 / 16 = 9 см
ВС = BD + DC = 16 + 9 = 25 см
Из прямоугольного треугольника АВС по теореме Пифагора:
AC = √(BC² - AB²) = √(625 - 400) = √225 = 15 см
cos∠C = AC / BC = 15 / 25 = 3/5 = 0,6
2. ΔABD: ∠ADB = 90°,
cos∠A = AD / AB
AD = AB · cos 41° ≈ 12 · 0,7547 ≈ 9,1 см
ΔADH: ∠AHD = 90°,
sin∠A = DH / AD
DH = AD · sin41° ≈ 9,1 · 0,6561 ≈ 6 см
Sabcd = AB · DH ≈ 12 · 6 ≈ 72 см²