т.к внешний угол при вершине В равен 66 то угол В будет равен 180-66=114, а т.к АВ=ВС то треугольник АВС ровнобедренный,это значит что углы при основании равны. Отсюда угол а будет равен (180-114) : 2=33. ОТВЕТ 33
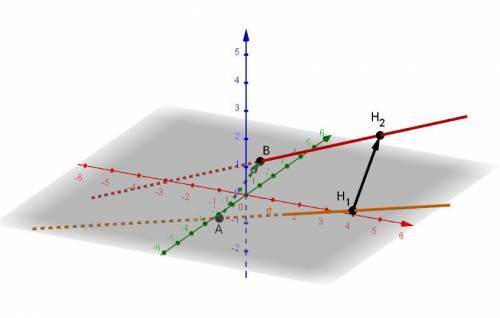
Даны уравнения прямых:
(x + 1)/3 = y/(-1) = (z + 1)/(-1) и (x + 1)/2 = (y - 3)/(-1) = z/1 .
1) Перепишем уравнения первой прямой в параметрической форме:
x = 3t - 1,
y = -t,
z = t - 1.
Примем точку Н1 как точку пересечения первой заданной прямой и общего перпендикуляра.
Её координатам соответствует вполне конкретное значение параметра, обозначим его через to . Тогда координаты точки запишутся в виде:
x = 3to - 1,
y = -to,
z = to - 1.
Аналогично для точки Н2 получим
x = 2so - 1,
y = -so + 3,
z = -so.
2) Находим вектор Н1Н2 по двум принципам.
Н1Н2 = p как результат векторного произведения направляющих векторов заданных прямых (ведь он перпендикулярен обеим прямым).
i j k | i j
3 -1 1 | 3 -1
2 -1 1 | 2 -1 = -1i + 2j - 3k -3j + 1i + 2k = 0i - 1j - 1k.
p = (0; -1; -1).
С другой стороны, вектор Н1Н2 проходит через 2 точки, координаты которых заданы в пункте 1.
Н1Н2: (2so - 3to; -so + to + 3; so - to + 1).
Поскольку направляющие векторы коллинеарны, то один вектор линейно выражается через другой с некоторым коэффициентом пропорциональности «лямбда»:
(2so - 3to; -so + to + 3; so - to + 1) = λ(0; -1; -1).
Или покоординатно:
2so - 3to = λ*0;
-so + to + 3 = λ*(-1);
so - to + 1 = λ*(-1)
Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными , которая стандартно разрешима, например, методом Крамера.
so to λ B
2 -3 0 0 Определитель -2
-1 1 1 -3
1 -1 1 -1
Заменяем 1-й столбец на вектор результатов B:
0 -3 0
-3 1 1 Определитель -6
-1 -1 1
Заменяем 2-й столбец на вектор результатов B:
2 0 0
-1 -3 1 Определитель -4
1 -1 1
Заменяем 3-й столбец на вектор результатов B:
2 -3 0
-1 1 -3 Определитель 4
1 -1 -1
so= -6/ -2 = 3
to= -4/ -2 = 2
λ= 4/ -2 = -2.
Отсюда находим координаты точек:
Н1 = (5; -2; 1) и Н2 = )5; 0; 3).
Вектор Н1Н2 = (0; 2; 2) и его длина √(0²+ 2² + 2²) = √8 = 2√2.
Даны прямая (x-3)/2=(y+2)/4=z/1 и точка M(2;-1;2).
M1(3;-2;0) -уже заданная точка по условию задачи, которая принадлежит прямой .
Вектор ММ1{3-2;(-2)-(-1);0-2}={1;-1;-2}
q1{2;4;1} - направляющий вектор прямой (по условию задачи)
Векторы {x-3;y+2;z}, МM1, q1 - компланарны. Поэтому для них можно записать
x - 3 y + 2 z (x - 3)*(-1) + (y + 2)*(-4) + z*4 +
1 -1 -2 + (y + 2)*(-1) + (x - 3)*8 + z*2 =
2 4 1 = 0. = 7x - 21 - 5y - 10 + 6z.
Раскрыв определитель системы, приходим к уравнению
7x - 5y+ 6z - 31 = 0.
Это и будет искомое уравнение плоскости, которая проходит через точку M и прямую.
57.
180-66 и делить на два